Abitur 1999 Leistungskurs Mathematik Gruppe I, Analysis, Aufgabe 1
Eine gedämpfte Schwingung kann durch folgende Funktion dargestellt werden (k > 0, omega > 0, reell):
![]()
a) Zeigen Sie, daß y(t) folgende Differentialgleichung erfüllt:
![]()
Bestimmen Sie die Nullstellen, die Extrempunkte und die Wendestellen für allgemeine Parameter und zeichnen Sie y(t) für k=0, 1 und 5 und omega=2*Pi.
Wie verändert der Parameter k die Lage der Extrema? Besitzt die Kurvenschar y(k,t) gemeinsame Punkte? Besitzt die Kurvenschar y'(k,t) gemeinsame Punkte?
b) Zeigen Sie, daß die Maxima der Funktion eine geometrische Folge bilden und geben Sie diese Folge in rekursiver und expliziter Schreibweise für k=1 und omega=1 an.
Wie groß ist der Grenzwert der zugehörigen geometrischen Reihe?
Die Flächenstücke, die y(t) oberhalb der t-Achse mit der t-Achse einschließt, haben näherungsweise zwei Drittel des Inhalts der Rechtecke, die so hoch sind wie die Maxima und so breit wie der Abstand zweier Nullstellen. Wie groß ist also der Inhalt der Fläche, die oberhalb der positiven t-Achse liegt? Die Näherung gilt auch für die Minima. Wie groß ist dann
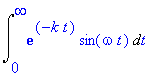
näherungsweise? Berechnen Sie obiges Integral exakt für allgemeine Parameter und vergleichen Sie mit der Näherung.
c) Neben dem exponentiellen Abklingen (expo) einer Schwingung kommt auch ein Abklingen vor, das umgekehrt proportional zur Zeit ist (gebr). Man kann die Typen des Abklingens so vergleichen:
![]()
Skizzieren Sie die beiden Kurven für a=1.
Geht man von der reellen Zeit t zu einer Folge natürlicher Zahlen n > 1 über und setzt man
a > -1 (reell) voraus, so läßt sich zeigen, daß gilt:
![]()