Für das Differenzieren gibt es zwei Befehle: diff() für Ausdrücke (Terme) und den D-Operator für Funktionen.

Ausdrücke werden mit diff(term,var) partiell nach der im zweiten Argument angegebenen Variablen abgeleitet:

> Diff(a*x^3+b*x^2+c*x,x)=diff(a*x^3+b*x^2+c*x,x);

> Diff(a*x^3+b*x^2+c*x,a)=diff(a*x^3+b*x^2+c*x,a);

>

>

Da der Ausdruck meistens im Zusammenhang mit einer Funktion vorkommt (als Funktionsterm), ist eine korrekte Handhabung erforderlich, bzw. es gibt eine Reihe von Fehlerquellen:

> term:=x^2;

> diff(term,x);

Bildet man aus dem Term (nach der frühen Bindung) eine Funktion, so sollte man unapply() verwenden und nicht die Pfeilschreibweise:

> funktion:=unapply(term,x);

> pfeil:=x->term;

> funktion(etwas); pfeil(etwas);

Die Zuordnung ist in pfeil() immer x^2, deshalb erhält man nur für diese Variable die richtige Ableitung:

> diff(funktion(z),z); diff(pfeil(etwas),x); diff(pfeil(x),etwas);

Eine weitere Fehlerquelle ist es, nur den Funktionsnamen zu erwähnen, der dann als Term interpretiert wird:

> diff(funktion,x); diff(pfeil,x); diff(pfeil,pfeil);

>

Ableitung an einer Stelle

> eval(Diff(x^3+x^2+x,x),x=0)=eval(diff(x^3+x^2+x,x),x=0);

> subs(x=0,diff(x^3+x^2+x,x));

Auch hier gibt es Stolpersteine, weil sich das Ableiten und das Einsetzen nicht vertauschen lassen

> su:=subs(x=0,diff(f(x),x));

> ev:=eval(diff(f(x),x),x=0);

> f:=sin; ev; su;

Error, wrong number (or type) of parameters in function diff

> f:='f':

> (x->diff(x^2,x))(1);

Error, (in unknown) wrong number (or type) of parameters in function diff

> (x->diff(x^2,x))(etwas);

> unapply(diff(x^2,x),x)(1);

Merke: Mit unapply() und eval() ist man auf der sicheren Seite, während die Pfeilschreibweise und subs() zu unbeabsichtigten Ergebnissen führen können.

>

>

Höhere Ableitungen

> diff(x^3+x^2+x,x,x);

Oder kürzer mit dem $-Operator

> diff(x^3+x^2+x,x$3);

>

Bei automatisierten Berechnungen empfiehlt sich die Variante diff(term, [vars]), mit der auch eine leere Variablenliste angegeben werden kann:

> for var in [[],[x],[x,x]] do

> diff(x^3+x^2+x,var); od;

> seq(diff(x^3,[x$i]),i=-2..5);

>

Ableitungsregeln

> diff(a*f(x)+b*g(x),x);

> diff(f(x)*g(x),x);

> simplify(diff(f(x)/g(x),x));

> diff( f(g(x)), x);

Bei der Kettenregel erscheint der D-Operator für die vollständige Ableitung (s.u.).

>

>

Die Variablen nach denen abgeleitet wird, werden als unabhängig betrachtet

> diff( (x^2+y^3)^4, x, y);

> diff( (x^2+y^3)^4, x);

Abhängigkeiten könnnen z.B. mit y(x) formuliert werden

> diff( (x^2+y(x)^3)^4, x);

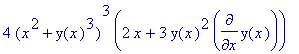
> alias(y=y(x)):

> diff( (x^2+y^3)^4, x);

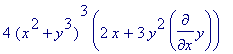
> alias(y=y);

> diff( f(x,y,z), x$2,y,z$2);

>

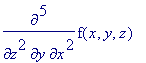
> diff( f(x,z), x$2,y,z$2);

>

>

Ein kleines Beispiel

> restart;

> `diff/f` := proc(x,dx) -f(2*x) * dx; end:

> diff( f(x), x);

> diff(f(x), y);

> diff( f(n), n$3);

>

>

Wenn die Abhängigkeit von Variablen implizit definiert ist

> f:=x^2+y^2=1;

erhält man mit implicitdiff() die Ableitung

> implicitdiff(f,y,x);

ebenfalls implizit aber ohne Umwege:

> solve(f,y);

> diff(%[1],x);

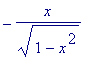
Ausführlicher

> implicitdiff({f},{y(x)},{y},x);

> implicitdiff({f},{y(x)},{y},x, notation=Diff);

Das gleiche Resultat mit diff and solve (diff läßt sich auch auf Gleichungen anwenden):

> diff(x^2+y(x)^2=1,x);
solve(%, diff(y(x),x));

>

Höhere implizite Ableitungen

> f:= x^2*y^2*z^2=1:

> implicitdiff(f,z,x,y);

> implicitdiff({f}, {z(x,y)}, {z}, x,y);

> implicitdiff({f}, {z(x,y)}, {z}, x,y, notation=Diff);

>

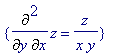
Der D-Operator erzeugt aus einer Funktion eine Funktion

> restart:

> D(x->x^2);

> D(x->x^2)(etwas);

> D(x->x^2)(5);

Mit Namensgebung

> y:=x->x^4;

> ys:=D(y);

> ys(9);

Oder für vordefinierte Funktionen

> D(sin);

Die Ordnung der Ableitung wird mit @@ angegeben

> yss:=(D@@2)(y);

> z:=(D@@0)(y)(10);

Aber nicht

> yss:=(D$2)(y);

sondern (s.u. Funktionen von mehreren Variablen)

> z:=D[1$2](y);

> z(8);

> z:=D[](y);

> z(8);

>

Weil für die Anwendung von Funktionsvorschriften folgende Regeln gelten

> (f+g)(x), (f*g)(x), (f/g)(x), (f@g)(x), 5(x);

lauten die Ableitungsregeln

> D(f+g);

> D(f*g);

> simplify(D(f/g));

> D(f@g);

Und nicht

> D(f(g));

> D(5);

>

Funktionen von mehreren Veränderlichen

> f:=(x,y)->sin(x)+cos(y)+sin(x*y);

> D[1](f);

> D[2](f);

> D[2](f)(alpha,beta);

> D[2$2](f);

> D[1$3,2$4](f);

> diff( f(x,y), x$3, y$4);

>

>

> restart:

> diff( f(x,y,z), x,y,z$2);

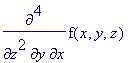
> convert(%, D);

> lprint(%);

D[1,2,3,3](f)(x,y,z)

> convert(%, diff);

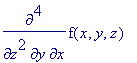
> lprint(%);

diff(diff(diff(diff(f(x,y,z),x),y),z),z)

>

>

> f := proc(x) local t0,t1,t2;
t0 := sin(x): t1 := cos(x):
t2 := (t0^2+t1+3)/(t1^3-t0);
sin(t2^2+1)*cos(t2^2-1);
end:

> f(x);

>

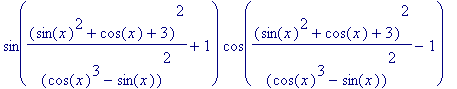
Ableiten des Funktionsterms mit diff

> fd1:=diff(f(x), x);

>

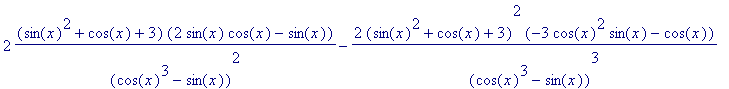
Erzeugen einer Prozedur für die Ableitung mit D

> fd2:=D(f);

>