fourw_10.html

fourw_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 4.1.2

Worksheet kino1_10.mws

c International Thomson Publishing 1995 filename: fourw.ms

Autor: Komma Datum: 28.3.94

Index:Wirkungsfunktion

Thema: Wirkungsprinzip, schwaches Extremum der Wirkungsfunktion.

Wurf und harmonischer Oszillator:

Näherungslösung durch Bestimmung des schwachen Extremums der

Wirkungsfunktion, wenn die Ortsfunktion als "Fourierreihe" angesetzt wird.

Vergleich der Reihenentwicklungen.

> restart;

> T:=m/2*v^2;

T := 1/2*m*v^2

> v:=diff(x(t),t);

v := diff(x(t),t)

> L:=T-V(x(t));

L := 1/2*m*diff(x(t),t)^2-V(x(t))

> S:=int(L,t=t0..t1);

S := int(1/2*m*diff(x(t),t)^2-V(x(t)),t = t0 .. t1)

> H:=T+V(x(t));

H := 1/2*m*diff(x(t),t)^2+V(x(t))

> t0:=0:

Überlagerung von n Oberschwingungen (n>2) , Kurve durch (0|0) und (t1|x1):

> n:=6;

> xx:=proc(t) local xl;

> xl:=0;

> for i to n do

mit dem Cosinus bekommt man die Randbed. ohne gleichf. Bewegung herein.

> xl:=xl+a||i*sin(i*Pi*t/t1)+b||i*cos(i*Pi*t/t1);

> od;

> RETURN(xl);

> end;

Warning, `i` is implicitly declared local to procedure `xx`

> xx(t);

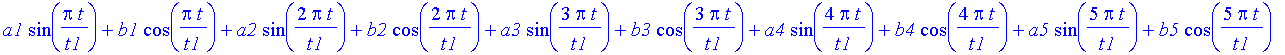
a1*sin(Pi*t/t1)+b1*cos(Pi*t/t1)+a2*sin(2*Pi*t/t1)+b2*cos(2*Pi*t/t1)+a3*sin(3*Pi*t/t1)+b3*cos(3*Pi*t/t1)+a4*sin(4*Pi*t/t1)+b4*cos(4*Pi*t/t1)+a5*sin(5*Pi*t/t1)+b5*cos(5*Pi*t/t1)+a6*sin(6*Pi*t/t1)+b6*cos(...

Zwei Koeffizienten (z.B. b1 und b2) lassen sich mit Hilfe der Bedingungen x(0)=0 und x(t1)=x1 durch die anderen Koeffizienten ausdrücken:

>

> solb:=solve({xx(0)=0,xx(t1)=x1},{b1,b2});

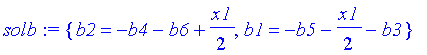
solb := {b2 = -b4-b6+1/2*x1, b1 = -b5-1/2*x1-b3}

>

> x:=t->subs(solb,xx(t));

>

> x(t);

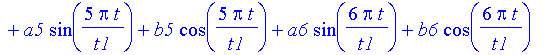
a1*sin(Pi*t/t1)+(-b5-1/2*x1-b3)*cos(Pi*t/t1)+a2*sin(2*Pi*t/t1)+(-b4-b6+1/2*x1)*cos(2*Pi*t/t1)+a3*sin(3*Pi*t/t1)+b3*cos(3*Pi*t/t1)+a4*sin(4*Pi*t/t1)+b4*cos(4*Pi*t/t1)+a5*sin(5*Pi*t/t1)+b5*cos(5*Pi*t/t1)...

V(x);

x(0);

lineares Potential / qudratisches Potential:

> k:='k':

> V:=proc(x)

> m*g*x;

> #1/2*k*x^2;

> end;

> #g:=1:

> #t1:=2:

> #S;

> Ss:=simplify(S,power);

> x(t);

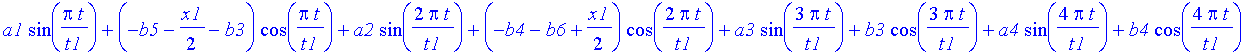
Notwendige Bedingung für schwaches Extremum: die partiellen Ableitungen der Wirkung nach den Formvariablen müssen verschwinden.

> sys:=seq(diff(Ss,a||j),j=1..n),seq(diff(Ss,b||j),j=3..n); # n>2

sys := -1/55440*m*(73920*Pi^2*x1-29568*Pi^2*b4-27720*Pi^3*a1+110880*g*t1^2-33792*Pi^2*b6)/t1/Pi, -1/55440*m*(337920*Pi^2*b5+36960*Pi^2*x1+473088*Pi^2*b3-110880*Pi^3*a2)/t1/Pi, -1/55440*m*(-133056*Pi^2*...

> #sys:=seq(diff(Ss,a.j),j=1..n); # n=2

> sol:=solve({sys},{a||(1..n),b||(3..n)}); #n>2

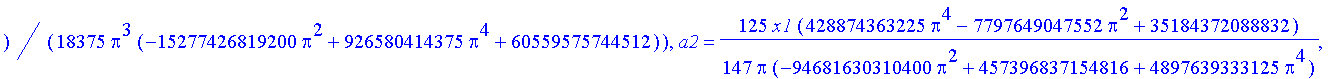
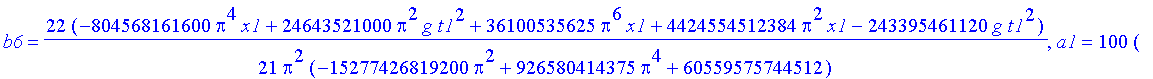
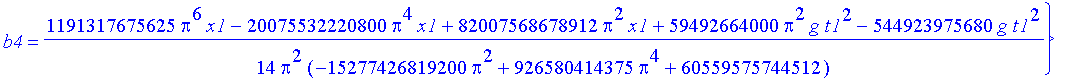
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$
$sol := {a6 = 275/441*x1*(-7078235996160*Pi^2+35184372088832+355973160375*Pi^4)/Pi/(-94681630310400*Pi^2+457396837154816+4897639333125*Pi^4), b3 = -125/14*x1*(26473726125*Pi^4-516731765760*Pi^2+25211458...$

> #sol:=solve({sys},{a.(1..n)}); #n=2

> x(t);

>

Lösung des Gleichungssystems in x(t) einsetzen:

> xs:=proc() subs(sol,x(t)); end;

> xs();

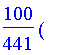
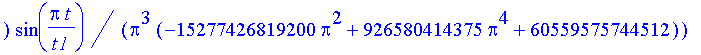
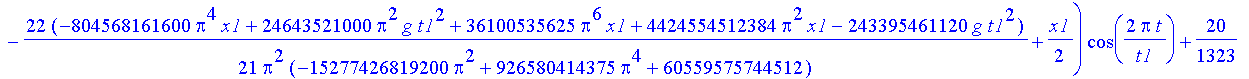
100/441*(10292984717400*Pi^6*x1-168385832681472*Pi^4*x1+659706976665600*Pi^2*x1-269652590936064*Pi^2*g*t1^2+1069824813826048*g*t1^2+16344878509575*Pi^4*g*t1^2)/Pi^3/(-15277426819200*Pi^2+926580414375*P...

>

simplify(xs(),power);

Federkonstante und Masse:

> k:=2: m:=1/4: g:=10:

Endpunkt:

> t1:=2:x1:=3:

xs();

Näherungslösung (schwaches Extremum)

> plot(xs(),t);

[Maple Plot]

Exakte Lösung der Newton-DGL:

> soly:=proc() rhs(dsolve({diff(y(t),t$2)=-diff(V(y),y)/m,y(0)=0,y(t1)=x1},y(t))); end;

Vergleich:

> plot({soly(),xs()},t=0..t1+1);

[Maple Plot]

> soly();

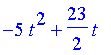
-5*t^2+23/2*t

diff(V(y),y);

V(x(t));

Vergleich des Polynoms mit der Reihenentwicklung

> evalf(series(soly(),t,10));

> evalf(series(xs(),t));

Anmerkungen: Der Lösungsansatz wird mit der Periode t1 gemacht. Deshalb erhält man auch bei quadratischem Potential (Oszillator) nicht die exakte Lösung, man kann aber die Reihenentwicklungen vergleichen. Natürlich kann man mit t1 (im Argument der Winkelfunktionen) experimentieren ...

>

komma@oe.uni-tuebingen.de