Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 2.1.8
Worksheet kino3_10.mws
| > |
c International Thomson Publishing Bonn filename: kino3
Autor: Komma Datum: 3.7.94
Thema: Kinematik - dreidimensional
Zur Beschreibung einer Bewegung im dreidimensionalen Raum können die Ortsfunktionen in einer Liste zusammengefaßt werden. Der Typ <vector wird *nicht* benötigt, er ist sogar eher hinderlich, z.B. bei der Ausgabe oder bei der Differentiation. Insofern ist der Befehl <vector() etwas irreführend, weil er suggeriert, daß er verwendet werden *muß*. Dabei bewirkt er nichts anderes, als die Bildung eines eindimensionalen arrays, dessen Indizes mit 1 beginnen. Listen können aber einfacher gehandhabt werden: Für ihre Ausgabe genügt die Angabe des Namens (ohne print) und der <diff-Operator kann ohne <map angewendet werden. Der Zugriff auf ein Listenelement erfolgt wie üblich durch die Angabe des Index in eckigen Klammern.
| > | restart; |
| > | r:=[x(t),y(t),z(t)]; |
![]()
| > | v:=diff(r,t); |
![]()
| > | a:=diff(v,t); a[3]; |
![a := [diff(x(t),`$`(t,2)), diff(y(t),`$`(t,2)), diff(z(t),`$`(t,2))]](kino3/kino3_103.gif)
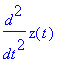
Als einfaches Beispiel können wir zunächst die Wurfbewegung dreidimensional behandeln.
| > | x:=t->vx0*t: y:=t->vy0*t: z:=t->vz0*t-1/2*g*t^2: |
| > | r;v;a; |
![]()
![]()
![]()
Interessiert man sich für die Bahngleichung (z.B. die z-Koordinate als Funktion der x- oder y-Koordinate), so kommt man am schnellsten zum Ziel, wenn man sich ein Gleichungssystem aufstellt, und die Zeit mit <solve eliminieren läßt. Dabei können allerdings die alten Namen der Koordinaten nur auf einer Seite der Gleichung verwendet werden.
| > | solve({x(t)=xx,y(t)=yy,z(t)=zz},{t,xx,zz}); |
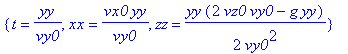
Umformung eines Teils der Lösung (der Index bezieht sich auf die *aktuelle* Ausgabe der vorangehenden Menge!):
| > | expand(%[2]); |
![]()
Auch die Umkehrfunktion läßt sich so finden:
| > | solve({x(t)=xx,z(t)=zz},{t,xx}); |
![]()
Dabei ist <RootOf() der Platzhalter für die Lösung der entsprechenden Gleichung in der Variablen _Z. Man kann sich diese Lösungen (meistens) mit <allvalues anzeigen lassen.
| > | allvalues(%); |
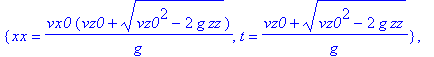
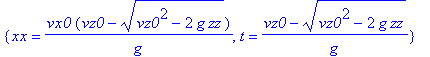
Zur Darstellung der Raumkurve verwendet man den Befehl <spacecurve. Aus der dreidimensionalen Darstellung kann man durch ziehen mit der Maus die Perspektive so verändern, daß die Blickrichtung parallel zu einer Achse liegt. Dann sieht man die Abhängigkeit einer Koordinate von einer anderen zweidimensional.
| > | with(plots): |
read `fig.m`:opt3d;
vtitle:=Wurf_3d: vzlab:=hoch: vxlab:=breit: vylab:=tief:
pspl(`p1kino3.ps`):winpl():
| > | vx0:=1: vy0:=-2: vz0:=6: g:=10: |
| > | spacecurve(r,t=0..1,scaling=constrained,axes=normal); |
![[Maple Plot]](kino3/kino3_1013.gif)
Die zweidimensionale Darstellung läßt sich auch mit einem parametrischen Plot erreichen.
winpl():vtitle:=Wurf_2d:vylab:=hoch:
pspl(`p2kino3.ps`):winpl():
| > | plot([x(t),z(t),t=0..2]); |
![[Maple Plot]](kino3/kino3_1014.gif)
Natürlich wird Maple auch mit anspruchsvolleren Funktionen fertig:
| > | unassign('k','x0','y0','z0'); |
| > | x:=t->x0*cos(t)*exp(-k*t): y:=t->y0*sin(t): z:=t->z0*sin(5*t): |
| > | r;v;a; |
![]()
![]()
![]()
| > | k:=0.1: x0:=2: y0:=3: z0:=5: |
pspl(`p3kino3.ps`):vtitle:=Raumkurve:xtick:=0:ytick:=0:ztick:=0:
| > | spacecurve(r,t=0..2*Pi,scaling=constrained,axes=framed,numpoints=100,orientation=[30,10]); |
![[Maple Plot]](kino3/kino3_1018.gif)
Oder wieder parametrisch:
pspl(`p4kino3.ps`):vtitle:=parametrisch:
| > | plot([y(t),z(t),t=0..2*Pi]); |
![[Maple Plot]](kino3/kino3_1019.gif)
| > |
Auch hier wieder die Bahnkurve, die sich für ganzzahlige Frequenzenverhältnisse als einfaches Polynom entpuppt:
| > | solve({y(t)=yy,z(t)=zz},{t,zz});# allvalues(%)[1]; |
![]()
Für die transzendente Gleichung z=z(x) findet auch Maple keine Lösung, die graphische Darstellung ist aber im parametrischen Plot möglich, wenn Sie im obigen Befehl y durch x ersetzen
| > | plot([x(t),z(t),t=0..2*Pi]); |
![[Maple Plot]](kino3/kino3_1021.gif)
Der parametrische Plot ist aber auch ein gutes Mittel zur Darstellung von Phasenportaits:
vtitle:=Schnecke:pspl(`p5kino3.ps`):
| > | plot([x(t),v[1],t=0..5*Pi]); |
![[Maple Plot]](kino3/kino3_1022.gif)
pspl(`p6kino3.ps`):vtitle:=z_von_a:vxlab:=`a[1]`:xtick:=2:vylab:=`z(t)`:ytick:=2:winpl():
| > | plot([a[1],z(t),t=-1..1]); |
![[Maple Plot]](kino3/kino3_1023.gif)
| > |
Mit Leichtigkeit lassen sich so alle nur erdenklichen Kombinationen der oben definierten Funktionen darstellen. Beachten Sie dabei auch, daß die Reihenfolge der Argumente wesentlich ist, daß also Funktion und Umkehrfunktion dargestellt werden kann.
| > |
| > |
| > |
komma@oe.uni-tuebingen.de