maschine_10.mws
Moderne Physik mit Maple
PDF-Buch
Moderne Physik mit Maple
Update auf Maple 10
Kapitel 2.2.6
Worksheet maschine_10.mws
c International Thomson Publishing Bonn 1995 filename: maschine.ms
Autor: Komma Datum 4.6.94
Thema: Der Schlußstein des Newton-Kapitels. Mit diesem worksheet und den Prozeduren procnewt.m und procnumn.m können alle Bewegungsgleichungen eines Massenpunktes gelöst werden.
Der Befehl dsolve(), die Handhabung von Packages, Funktionen und Plots (insbes. im Zusammenhang mit dsolve()) haben sich seit Maple V mehrfach geändert. Dieses Worksheet ist eine "Minimalversion", zur Sicherung des Übergangs zwischen den Releases von Maple V bis Maple 10.
Vorsicht: Die Prozeduren verwenden globale Variablen, die mit reset() und resetn() zurückgesetzt werden.
Geschlossenene Lösung
Vorbereitung
| > |
restart;with(linalg):with(student):with(plots):
|
| > |
newton:=proc(F) global x,y,z,r,v,a,xx,yy,zz,rf,vf,af,sol,sys;
|
| > |
r:=vector([x(t),y(t),z(t)]);
|
| > |
sol:=dsolve(sys,{x(t),y(t),z(t)},method=laplace);
#sol:=dsolve(sys,{x(t),y(t),z(t)});
|
| > |
if sol=NULL then sol:=dsolve(sys,{x(t),y(t),z(t)}) fi;
|
| > |
if sol=NULL then RETURN(`keine Loesung gefunden`) fi;
|
| > |
xx:=makeproc(x(t),t): yy:=makeproc(y(t),t): zz:=makeproc(z(t),t):
|
| > |
rf:=makeproc(map(eval,r),t); vf:=makeproc(map(eval,v),t); af:=makeproc(map(eval,a),t);
|
| > |
x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0';
|
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_101.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_102.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_103.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_104.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_105.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_106.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_107.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_108.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_109.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1010.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1011.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1012.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1013.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1014.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1015.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1016.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1017.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1018.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1019.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1020.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1021.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1022.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1023.gif)
![newton := proc (F) global x, y, z, r, v, a, xx, yy, zz, rf, vf, af, sol, sys; r := linalg:-vector([x(t), y(t), z(t)]); v := map(diff,r,t); a := map(diff,v,t); sys := equate(m*a,F); sol := dsolve(sys,{x...](maschine/maschine_1024.gif)
Zwei reset-Prozeduren sparen Schreibarbeit und im Kraftgesetz müssen Funktionen nicht mehr unausgewertet gesetzt werden.
| > |
reset:=proc() unassign('x(t)','y(t)','z(t)','x0','vx0','y0','vy0','z0','vz0','Fx','Fy','Fz','m');
|
| > |
x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0':
|
| > |
resetn:=proc() unassign('x','y','z','xn(t)','yn(t)','zn(t)','x0n','vx0n','y0n','vy0n','z0n','vz0n','Fx','Fy','Fz','m','sys','sysn');
|
| > |
#xn(0):='x0n': D(xn)(0):='vx0n': yn(0):='y0n': D(yn)(0):='vy0n':zn(0):='z0n': D(zn)(0):='vz0n':
|
Es war einmal...:
Die folgenden Einträge können mit F5 zeilenweise zu Text oder Input getoggelt werden. Wenn Sie immer nur eine Kraft als Input führen, springt der Cursor automatisch zum Aufruf der Lösungsprozedur newton(F). Dies ist eine bewährte Methode des Arbeitens mit Worksheets: Man hat alle Informationen am Bildschirm und kann mit dieser offenen Struktur am besten experimentieren. Wer eine kompaktere Formulierung wünscht, kann den einzelnen Krafgesetzen Namen geben und sie z.B. in einer table führen, oder in einer Prozedur, die diese Namen auswertet. Dann muß der Benutzer wirklich nur noch drei Angaben machen: Kraft (Auswahl aus einem Katalog) - Anfangsbedingungen - Lösung, hat aber bei diesem Fertigangebot nicht mehr die Möglichkeit des direkten Zugriffes, wenn er etwas ändern will.
Jetzt mit Hyperlinks zur Lösung der DGL.
Konstante Kraft
| > |
reset(); F:=vector([1,2,-3]);
|
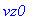
![F := vector([1, 2, -3])](maschine/maschine_1027.gif)
DGL lösen
Lineares Kraftgesetz
(in x-Richtung ;-))
| > |
reset(); F:=[-x(t),2,3];
|
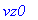
![F := [-x(t), 2, 3]](maschine/maschine_1029.gif)
DGL lösen
Lineares Kraftgesetz mit Dämpfung
| > |
reset(); F:=vector([Fx-x(t)-v[1],Fy,Fz]);
|
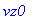
![F := vector([Fx-x(t)-diff(x(t),t), Fy, Fz])](maschine/maschine_1031.gif)
DGL lösen
Wurf mit Luftwiderstand
lineares Widerstandsgesetz:
| > |
reset();
vb:=sqrt(v[1]^2+v[2]^2+v[3]^2);
m:='m':g:='g':k:='k':
F:=vector([-k*v[1],-k*v[2],-m*g-k*v[3]]);
|
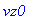
![vb := (v[1]^2+v[2]^2+v[3]^2)^(1/2)](maschine/maschine_1033.gif)
![F := vector([-k*v[1], -k*v[2], -m*g-k*v[3]])](maschine/maschine_1034.gif)
DGL lösen
*** Elektron im E-B-Feld:
Definition der Felder:
unassign('Ex','Ey','Ez','Bx','By','Bz','vl','rr'):
El:=vector([Ex,Ey,Ez]);
B:=vector([Bx,By,Bz]);
reset();
rr:=[x(t),y(t),z(t)];
vl:=map(diff,rr,t);
reset(); F:=q*(El+crossprod(vl,B));
Bx:=0:By:=0:Bz:=2:
Ex:=0:Ey:=-5:Ez:=1/10:
m:=1:q:=1:
![El := vector([Ex, Ey, Ez])](maschine/maschine_1035.gif)
![B := vector([Bx, By, Bz])](maschine/maschine_1036.gif)
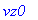
![rr := [x(t), y(t), z(t)]](maschine/maschine_1038.gif)
![vl := [diff(x(t),t), diff(y(t),t), diff(z(t),t)]](maschine/maschine_1039.gif)
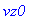
![F := El+vector([diff(y(t),t)*Bz-diff(z(t),t)*By, diff(z(t),t)*Bx-diff(x(t),t)*Bz, diff(x(t),t)*By-diff(y(t),t)*Bx])](maschine/maschine_1041.gif)
DGL lösen
***
Mathematisches Pendel (bevor Sie plotten, sollten Sie nachschauen, was newton(F) antwortet). Macht Ärger mit method=laplace.
| > |
reset(); F:=vector([-sin(x(t)),2,3]);
|
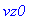
![F := vector([-sin(x(t)), 2, 3])](maschine/maschine_1043.gif)
DGL lösen
Aufruf der Prozedur "newton"
, die eine geschlossene Lösung sucht. Wenn eine Lösung gefunden wurde, stehen anschließend die Lösungsvektoren rf (Ort), vf (Geschwindigkeit) und af (Beschleunigung) zur Verfügung, die mit rf(Zeit) oder mit rf(Zeit)[Komponente] angesprochen werden können, dabei gilt: rf(t)=[x(t),y(t),z(t)].
![t -> [x0+m*vx0*(1-exp(-k*t/m))/k, y0+m*vy0*(1-exp(-k*t/m))/k, z0+1/k^2*m^2*g-(vz0*k+m*g)*m/k^2*exp(-k*t/m)-1/k*m*(g*t-vz0)]](maschine/maschine_1044.gif)
| > |
# diese Zeile bremst nur den Cursor, damit Sie sich die Lösung in Ruhe anschauen können
|
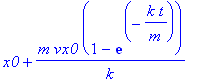
Die folgenden Anfangsbedingungen
sind so gewählt, daß für alle hier aufgeführten Beispiele "etwas Vernünftiges" zu sehen ist (das ist natürlich auch eine Frage des Maßstabes - in den Plots)
| > |
m:=1: x0:=0: vx0:=2: y0:=0:vy0:=1: z0:=0:vz0:=10:
|
| > |
Fx:=0:Fy:=0:Fz:=0: g:=10:k:=1:
|
x0:=0:vx0:=0:y0:=0:vy0:=5:z0:=0:vz0:=0:
Anfangsbedingungen für Bewegung in E-B
m:=1: x0:=0: vx0:=2: y0:=0:vy0:=1: z0:=0:vz0:=10:Fx:=0:Fy:=0:Fz:=0:
x-t-, v-t-, a-t-Diagramm
(Bitte die passenden Indizes je Beispiel selbst eintragen / ändern)
| > |
rf(t); # Kontrollausgabe
|
![[2-2*exp(-t), 1-exp(-t), 20-20*exp(-t)-10*t]](maschine/maschine_1046.gif)
| > |
plot({rf(t)[1],vf(t)[1],af(t)[1]},t=0..4);
|
![[Maple Plot]](maschine/maschine_1047.gif)
Falls Sie zwei Bewegungstypen vergleichen wollen (z.B. Wurf mit und ohne Luftwiderstand), können Sie hier eine Plotstruktur unter "real" und die andere unter "ideal" abspeichern und mit display gemeinsam anzeigen. Dazu müssen Sie allerdings die Bewegungsgleichung zweimal mit den entsprechenden Kraftgesetzen lösen.
Beispiel: Wurf ohne und mit Luftwiderstand
| > |
ideal:=plot({rf(t)[3],vf(t)[3],af(t)[3]},t=0..4):ideal;
|
![[Maple Plot]](maschine/maschine_1048.gif)
| > |
realp:=plot({rf(t)[3],vf(t)[3],af(t)[3]},t=0..4):
|
![[Maple Plot]](maschine/maschine_1049.gif)
| > |
display({realp,ideal});
|
![[Maple Plot]](maschine/maschine_1050.gif)
Falls Sie die Darstellung für das lineare Kraftgesetz unter "real" abgespeichert haben, können Sie sie weiter unten (bei den numerischen Lösungen) mit dem quadratischen Widerstandsgesetz vergleichen.
Raumkurve
| > |
myoptions:=axes=normal,labels=['x','y','z'],orientation=[70,60],scaling=constrained:
|
| > |
spacecurve(rf(t),t=0..3,myoptions,color=red);
|
![[Maple Plot]](maschine/maschine_1051.gif)
Phasenpotrait (es gibt 9 über 2 Möglichkeiten)
| > |
plot([rf(t)[3],vf(t)[3],t=-1..5],scaling=constrained);
|
![[Maple Plot]](maschine/maschine_1052.gif)
Numerische Lösungen
Es war einmal?...
In der derzeitigen Version von Maple V Release 3 wird die Lösung immer vom zuletzt benützten Zeitpunkt ausgehend berechnet. Wenn man also z.B. bei einem Plot schon bis zur Zeit t = 8 rechnen ließ, und beim nächsten Plot wieder bei t = 0 anfängt, muß erst wieder "zurückgerechnet" werden - mit einem entsprechenden Verlust an Genauigkeit und einem Entsprechenden Aufwand an Rechenzeit. In der nächsten Release soll der Anwender mehr Kontrolle über das Verhalten von Maple in diesem Punkt bekommen. Wundern Sie sich also nicht, wenn Ergebnisse nicht reproduzierbar sind, oder ewig kein Plot erscheint, oder Fehlermeldungen, die "vorher noch nie da waren". Ein neuer Aufruf von numnewton hilft meistens. Denken Sie an diese Warnung vor allem bei dem Befehl odeplot.
Vorbereitung
| > |
#restart:with(linalg):with(student):with(plots):
|
| > |
numnewton:=proc(F,ini) global rn,vn,an,xn,yn,zn,rfn,vfn,afn,soll,solp,sysn;
|
| > |
unassign('xn(t)','yn(t)','zn(t)','x0','vx0','y0','vy0','z0','vz0');
|
| > |
rn:=vector([xn(t),yn(t),zn(t)]);
|
| > |
ersetze:={xn='x',yn='y',zn='z'};
resetze:={x=xn,y=yn,z=zn};
|
| > |
sysn:=subs(ersetze,equate(m*an,F));
#print(sysn);
|
| > |
solp:=dsolve(sysn union subs(ersetze,ini),numeric,output=procedurelist);
|
| > |
#print(solp);
soll:=subs(resetze,dsolve(sysn union subs(ersetze,ini),numeric,output=listprocedure));
|
| > |
rfn:=subs(soll,op(rn));
|
| > |
vfn:=subs(soll,op(vn));
|
| > |
#af:=subs(soll,evalm(op(F)/m));
|
| > |
#af:=t->map(eval,subs(solp(t),evalm(F/m)));
|
Mit den vorangehenden Zuweisungen für af bekommt man Probleme: Es ist eine Frage der Priorität (Nichtkommutativität) von () und []. Man kann so zwar af() numerisch berechnen, aber nicht plotten (im Plot darf kein Argument angegeben werden). Auch lassen sich die folgenden drei Befehle nicht so ohne weiteres zusammenfassen (etwa mit for oder seq), aber so funktioniert wenigstens alles. Das sind eben die Eigenarten der Maple-Sprache. "Die Designer von Maple haben das so entschieden" (Monagan). Also Sonderlösung, insbes. für Phasenportraits mit af:
| > |
afn[1]:=t->map(eval,subs(solp(t),(subs(ersetze,F[1]/m))));
|
| > |
afn[2]:=t->map(eval,subs(solp(t),(subs(ersetze,F[2]/m))));
|
| > |
afn[3]:=t->map(eval,subs(solp(t),(subs(ersetze,F[3]/m))));
|
Warning, `ersetze` is implicitly declared local to procedure `numnewton`
Warning, `resetze` is implicitly declared local to procedure `numnewton`
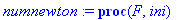
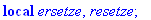
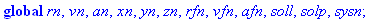
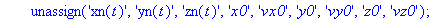
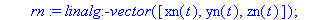

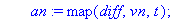
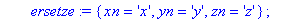
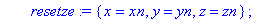
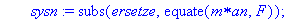
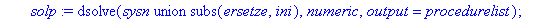
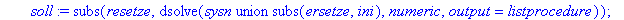
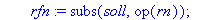
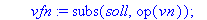
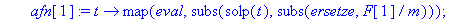
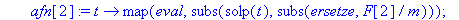
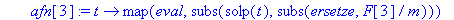

| > |
resetn:=proc() unassign('x','y','z','xn(t)','yn(t)','zn(t)','x0n','vx0n','y0n','vy0n','z0n','vz0n','Fx','Fy','Fz','m','sys','sysn');
|
| > |
#xn(0):='x0n': D(xn)(0):='vx0n': yn(0):='y0n': D(yn)(0):='vy0n':zn(0):='z0n': D(zn)(0):='vz0n':
|
| > |
reset:=proc() unassign('x(t)','y(t)','z(t)','x0','vx0','y0','vy0','z0','vz0','Fx','Fy','Fz','m');
|
| > |
x(0):='x0': D(x)(0):='vx0': y(0):='y0': D(y)(0):='vy0':z(0):='z0': D(z)(0):='vz0':
|
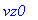
Die Anfangsbedingungen werden gleichzeitig mit der Kraft gesetzt, weil sie von der Lösungsprozedur benötigt werden. (Für die Keplerbewegung muß m=const (aber beliebig) gesetzt werden.)
*** konstante Kraft (als erste Übung - zum Vergleich mit der geschlossenen Lösung):
| > |
resetn(); F:=vector([1,2,-3]);
|
| > |
numini:={xn(0)=0,D(xn)(0)=2,yn(0)=0,D(yn)(0)=1,zn(0)=0,D(zn)(0)=10};
|
| > |
m:=1: Fx:=0:Fy:=0:Fz:=0:
|
![F := vector([1, 2, -3])](maschine/maschine_1072.gif)
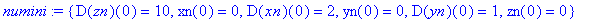
Numerische Lösung
*** Gedämpfte Schwingung
| > |
resetn(); F:=vector([Fx-xn(t)-vn[1],Fy,Fz]);
|
| > |
numini:={xn(0)=0,D(xn)(0)=2,yn(0)=0,D(yn)(0)=1,zn(0)=0,D(zn)(0)=0};
|
| > |
m:=1: Fx:=0:Fy:=0:Fz:=0:
|
![F := vector([Fx-xn(t)-diff(xn(t),t), Fy, Fz])](maschine/maschine_1074.gif)
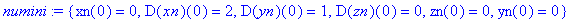
Numerische Lösung
*** Mathematisches Pendel (m stellvertretend für 1/Fallbeschleunigung):
| > |
resetn(); F:=vector([-sin(xn(t)),Fy,Fz]);
|
| > |
m:=1/3;Fx:=0: Fy:=0: Fz:=0:
|
| > |
numini:={xn(0)=0,D(xn)(0)=3,yn(0)=0,D(yn)(0)=0.8,zn(0)=0,D(zn)(0)=0.1};
|
![F := vector([-sin(xn(t)), Fy, Fz])](maschine/maschine_1076.gif)
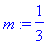
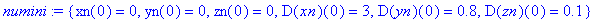
Numerische Lösung
*** ballistische Kurve (quadratisches Widerstandsgesetz)
| > |
vb:=sqrt(vn[1]^2+vn[2]^2+vn[3]^2);
|
| > |
resetn(); F:=vector([-k*vn[1]*vb,-k*vn[2]*vb,-m*g-k*vn[3]*vb]);
|
| > |
numini:={xn(0)=0,D(xn)(0)=2,yn(0)=0,D(yn)(0)=1,zn(0)=0,D(zn)(0)=10};
|
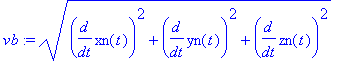
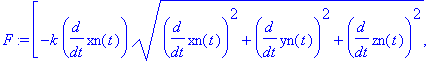
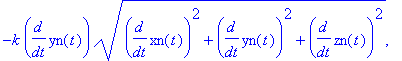
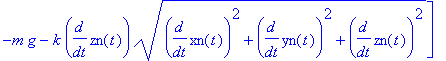
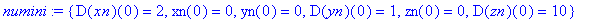
Numerische Lösung
*** Zentralfeld (zunächst 1/r^2)
| > |
rb:=xn(t)^2+yn(t)^2+zn(t)^2;
|
| > |
F:=vector([-m*xn(t)/rb^(3/2),-m*yn(t)/rb^(3/2),-m*zn(t)/rb^(3/2)]);
|
| > |
m:=1/3;Fx:=0: Fy:=0: Fz:=0:
|
| > |
numini:={xn(0)=1,D(xn)(0)=0,yn(0)=0,D(yn)(0)=0.8,zn(0)=0,D(zn)(0)=0.1};
|
geeigneter Parametersatz für Keplerbewegung: es ist gar nicht so einfach, ihn durch Probieren zu finden ... Fluchtgeschwindigkeit usw. Manchmal kommt auch die Fehlermeldung "falscher Parametertyp", dann wird wohl etwas imaginär ...
numini:={xn(0)=1,D(xn)(0)=0,yn(0)=0,D(yn)(0)=0.8,zn(0)=0,D(zn)(0)=0};
F();
sysn;
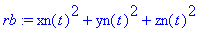
![F := vector([-m*xn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2), -m*yn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2), -m*zn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2)])](maschine/maschine_1085.gif)
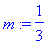
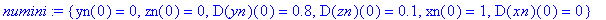
Numerische Lösung
Aufruf der Prozedur
![t -> map(eval,subs(solp(t),subs(ersetze,F[3]/m)))](maschine/maschine_1088.gif)
| > |
# diese Zeile bremst nur den Cursor, damit Sie sich die Ausgabe von oben in Ruhe anschauen können
|
sys;sysn;
Hier können Sie die numerische Lösung testen, indem Sie verschiedene Zeiten einsetzen ... und dann wieder zu t = 0 zurückgehen ...
rfn[3](0);
afn[3](0);
vfn[3](0);
Plots:
Wenn Sie zu Übungszwecken eine numerische Lösung mit der (zuvor berechneten) geschlossenen Lösung vergleichen wollen, so können Sie z.B. die folgenden Befehle aktivieren:
p1:=plot(xx(t),t=0..5):
p2:=odeplot(soll,[t,xn(t)],0..5,style=point,symbol=circle):
display({p1,p2});
Für die ballistische Kurve sollten nicht zu große Zeiten gewählt werden! m=1,g=10,k=1 -> t <= 4! (Es sind noch Optionen - maxerr ... auszunützen. Nach "zu großen Zeiten" ist die Lösung verpfuscht: numnewton neu laufen lassen)
x-t-, v-t-, a-t-Diagramm (Für die Darstellung der z-Komponenten bitte als Index 3 eintragen)
| > |
qreal:=plot({rfn[1],vfn[1],afn[1]},0..4):
|
![[Maple Plot]](maschine/maschine_1089.gif)
Falls Sie bei den geschlossenen Lösungen die Kurven des linearen Widerstandsgesetzes unter "real" abgespeichert haben, können Sie nun mit dem quadratischen W-Gesetz vergleichen:
| > |
display({realp,qreal});
|
Raumkurve
![[Maple Plot]](maschine/maschine_1090.gif)
| > |
odeplot(solp,[x(t),y(t),z(t)],0..4,axes=normal,color=red);
|
![[Maple Plot]](maschine/maschine_1091.gif)
Phasenportraits - incl. Bahn (nicht für ballistische Kurve, jedenfalls nicht mit negativen Zeiten und "zu großen Zeiten" t <= 4 bei den vorliegenden Parametern s.o.)
| > |
odeplot(soll,[x(t),y(t)],0..2);
|
![[Maple Plot]](maschine/maschine_1092.gif)
| > |
odeplot(solp,[y(t),x(t)],0..2);
|
![[Maple Plot]](maschine/maschine_1093.gif)
| > |
odeplot(solp,[x(t),diff(x(t),t)],0..2);
|
![[Maple Plot]](maschine/maschine_1094.gif)
***********
Alternative Art des Zugriffs auf die Lösungsgesamtheit, die Reihenfolge der procs ist wieder dem Zufall überlassen ... :
Für die Komponenten der Liste der Lösungsprozeduren verwendet man normale Plotbefehle:
| > |
plot({rhs(soll[1]),rhs(soll[2]),rhs(soll[3]),rhs(soll[4])},0..3);
|
![[Maple Plot]](maschine/maschine_1095.gif)
Phasenportraits (incl. Bahn)
| > |
plot([rhs(soll[4]),rhs(soll[5]),0..3]);
|
![[Maple Plot]](maschine/maschine_1096.gif)
Sonderfall des v-a-Phasenportraits: um "cannot evaluate boolean" zu vermeiden, muß die Auswertung der zu zeichnenden Funktion durch ' ' unterdrückt werden, bis von dem plot-Befehl für t eine Zahl eingesetzt wird. Diese Art des parametrischen Plots kann natürlich auch für alle anderen Phasenportraits benützt werden.
| > |
plot(['vfn[1](t)','afn[1](t)',t=0..2]);
|
![[Maple Plot]](maschine/maschine_1097.gif)
| > |
spacecurve([rhs(soll[2]),rhs(soll[4]),rhs(soll[6])],0..3,color=red);
|
![[Maple Plot]](maschine/maschine_1098.gif)
komma@oe.uni-tuebingen.de
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![t -> [x0+m*vx0*(1-exp(-k*t/m))/k, y0+m*vy0*(1-exp(-k*t/m))/k, z0+1/k^2*m^2*g-(vz0*k+m*g)*m/k^2*exp(-k*t/m)-1/k*m*(g*t-vz0)]](maschine/maschine_1044.gif)
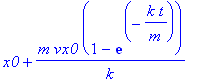
![]()
![[Maple Plot]](maschine/maschine_1047.gif)
![[Maple Plot]](maschine/maschine_1048.gif)
![[Maple Plot]](maschine/maschine_1049.gif)
![[Maple Plot]](maschine/maschine_1050.gif)
![[Maple Plot]](maschine/maschine_1051.gif)
![[Maple Plot]](maschine/maschine_1052.gif)
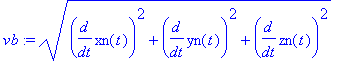
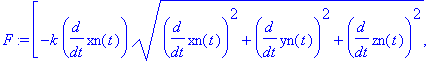
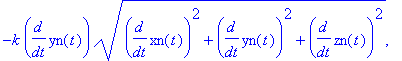
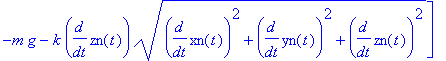
![F := vector([-m*xn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2), -m*yn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2), -m*zn(t)/(xn(t)^2+yn(t)^2+zn(t)^2)^(3/2)])](maschine/maschine_1085.gif)
![t -> map(eval,subs(solp(t),subs(ersetze,F[3]/m)))](maschine/maschine_1088.gif)
![[Maple Plot]](maschine/maschine_1089.gif)
![[Maple Plot]](maschine/maschine_1090.gif)
![[Maple Plot]](maschine/maschine_1091.gif)
![[Maple Plot]](maschine/maschine_1092.gif)
![[Maple Plot]](maschine/maschine_1093.gif)
![[Maple Plot]](maschine/maschine_1094.gif)
![[Maple Plot]](maschine/maschine_1095.gif)
![[Maple Plot]](maschine/maschine_1096.gif)
![[Maple Plot]](maschine/maschine_1097.gif)
![[Maple Plot]](maschine/maschine_1098.gif)