Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel A.2.1
Worksheet mld1g1_10.mws
| > |
DG 1. Ordnung mit konstanten Koeffizienten
Ein Überblick
(Aus 'Moderne Physik mit Maple' Komma, International Thomson Publishing Bonn 1995 filename: mld1g1.ms 24.7.94)
Die linearen Differentialgleichungen mit konstanten Koeffizienten gehören wohl zum wichtigsten Gleichungstyp der Physik. Sie erscheinen in weiten Bereichen als der Prototyp der Bewegungsgleichung einer deterministisch aufgefaßten Natur. Das reicht vom Zerfall und vom Wachstum über periodische Vorgänge, aber auch Diffusionsprozesse bis in die Quantenphysik. Es scheint einfach natürlich zu sein, daß zwischen der Änderung einer Größe und ihrem Momentanwert Proportionalitäten bestehen. Solche Zusammenhänge werden durch die Exponentialfunktion beschrieben aber nur dann in voller Allgemeinheit, wenn man komplexe Argumente zuläßt. Es ist das Anliegen dieser Kapitel, diese Zusammenhänge zu beleuchten. Wie schon im vorangehenden Abschnitt wird nicht beabsichtigt, eine komplette Theorie darzustellen, sondern die Möglichkeiten eines CAS auszunützen, um einen kleinen Streifzug durch die Welt der Exponentialfunktion zu machen. Die dabei geknüpften Assoziationen reichen von der Lösung der DGn über Diffrenzengleichungen und die geometrische Reihe bis hin zu Eigenwerten und Eigenvektoren. Sie können vom (inter-)aktiven Leser weiter verfolgt werden, indem er Parameter ändert, Darstellungsmöglichkeiten auslotet, einzelne Teile der worksheets umordnet und neu kombiniert.
Weil wir es mit "Bewegungen" zu tun haben, wählen wir die Zeit t als unabhängige Variable (und den "Ort" x als abhängige Variable).
Der Standard-Zugang zur linearen DG (mit konstanten Koeffizienten wird im Folgenden weggelassen) sieht gewöhnlich so aus. Die homogene DG ay' + by = 0 kann auch geschrieben werden als:
| > | restart; with(DEtools): with(plots): |
| > | dg:=diff(x(t),t)+k*x(t)=0; |
![]()
| > | dsolve(dg,x(t)); |
![]()
| > |
Je nach dem Vorzeichen von k liegt also exponentieller Zerfall oder exponentielles Wachstum vor. Das ist allgemein bekannt und man benötigt dafür kein CAS. Aber schon wenn man etwa den Zerfall einer radioaktiven Substanz eine Generation weiter verfolgen will, hat man wohl mit den herkömmlichen Methoden die Lösung nicht so schnell parat wie Maple:
| > |
| > | dgln:=diff(A(t),t)=-ka*A(t), |
| > | diff(B(t),t)= ka*A(t)-kb*B(t); |
![]()
| > | sol:=dsolve({dgln},{A(t),B(t)},method=laplace); |
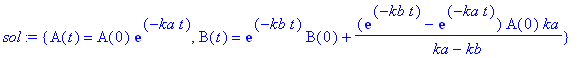
| > |
Mit dem Befehl DEplot3d() (Package DEtools) kann man sich einen schnellen Überblick über die Lösung verschaffen. Man erhält eine 3D-Darstellung, die man mit der Maus so drehen kann, daß A(t), B(t) oder B(A) zweidimensional dargestellt werden. Dabei ist B(A) das Phasenportrait, das man auch mit DEplot() oder phaseportrait() zusammen mit dem Richtungsfeld erhält. Die 3D-Darstellung ist aber sehr nützlich, weil sie eben die ganze Information enthält.
| > | ka:=1: kb:=2: |
| > | DEplot3d([dgln],[A(t),B(t)],0..10,{[A(0)=2,B(0)=0]},stepsize=0.1); |
![[Maple Plot]](mld1g1/mld1g1_105.gif)
| > |
| > | phaseportrait([dgln],[A(t),B(t)],0..10,{[0,2,0]},stepsize=0.1); |
![[Maple Plot]](mld1g1/mld1g1_106.gif)
| > |
Das Phasenportrait läßt eine quadratische Abhängigkeit von B von A vermuten. Muß das immer so sein? Aber wozu haben wir ein CAS?
Nach der Zuweisung mit assign() können die Lösungen aber auch "von Hand" weiterverarbeitet werden.
| > | ka:='ka': kb:='kb': |
| > | assign(sol); |
| > | A(t); |
![]()
| > | B(t); |
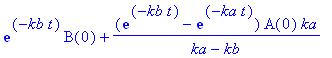
| > | tt:=solve(A(t)=A,t); |
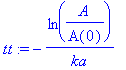
| > | subs(t=tt,B(t)); |
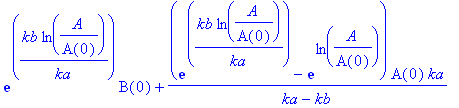
| > | expand(%); |
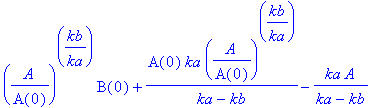
| > | simplify(%,power); |
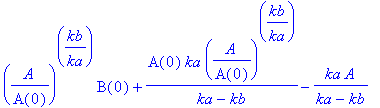
Also nur für kb/ka = 2 ein quadratischer Zusammenhang. Und ganz nebenbei läßt sich gleich auch noch die Frage klären, was für kb = ka passiert:
| > | limit(%,kb=ka); |

Plot der Aktivitäten für verschiedene Werte der Zerfallskonstante kb (spielen Sie mit ka und dem Laufbereich von kb ):
| > | ka:=1: kb:='kb': A(0):=2: B(0):=0: |
| > | plot({ka*A(t),seq(eval(kb*B(t)),kb=seq(0.3*ii,ii=1..9))},t=0..10); |
![[Maple Plot]](mld1g1/mld1g1_1014.gif)
| > |
Im vorangehenden Plot muß ka ungleich kb sein. Aber wie lautet für den Fall ka = kb die Funktion B(t)?
| > | ka:='ka': kb:='kb': |
| > | limit(B(t),kb=ka); |
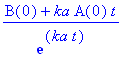
Mit der 3D-Darstellung umgeht man obige Einschränkung.
| > | ka:=1: kb:='kb': |
| > | plot3d({ka*A(t),kb*B(t)},kb=0..20,t=0..5,orientation=[145,45],style=hidden,axes=framed); |
![[Maple Plot]](mld1g1/mld1g1_1016.gif)
| > |
Man sieht so auf einen Blick die verschiedenen Gleichgewichtstypen (ideal: dB/dt = 0 - vgl. die zweite DG - , fortschreitend: kb > ka und sekulär kb >> ka ). Und natürlich läßt sich - einmal mehr - die Fragestellung leicht umkehren und beanworten: Für welche Wertepaare der Zerfallskonstanten bekommt man zu einem vorgegebenem Zeitpunkt die gleiche Gesamtaktivität und wann ist sie am größten? Wie hängt das Maximum vom Zeitpunkt ab? (Wenn man die Zeit variiert findet Maple ein paar unrealistische Inseln, die sich aber mit der grid -option ausbügeln lassen. Trick: Im Argument von A und B muß 't' geschrieben werden, damit nicht die Funktionen A(1) und B(1) geplottet werden - für t =1 z.B.)
| > | t:=1: |
| > | ka:='ka': kb:='kb': |
| > | contourplot({ka*A('t')+kb*B('t')},kb=0..20,ka=0..5,axes=boxed); |
![[Maple Plot]](mld1g1/mld1g1_1017.gif)
| > |
| > |
Wem zwei DGn nicht genug sind, der kann den Zerfall leicht ein paar Generationen weiter verfolgen:
| > | unassign('A','B','C','t'); |
| > | dgln:=diff(A(t),t)=-ka*A(t), |
| > | diff(B(t),t)= ka*A(t)-kb*B(t), |
| > | diff(C(t),t)= kb*B(t)-kc*C(t); |
![]()
| > | # diff(X(t),t)= kc*C(t)-kx*X(t); |
| > | sol:=dsolve({dgln},{A(t),B(t),C(t)},method=laplace); |
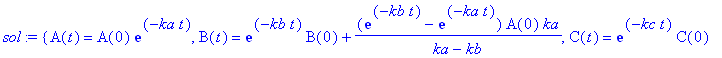
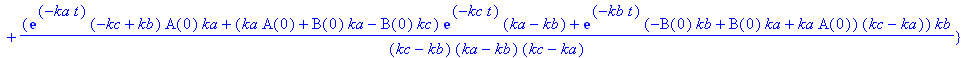
| > |
Spätestens hier lohnt sich der Einsatz eines CAS!
Aber:
Für Plots und Berechnungen: Eingabe konkreter Zahlen nur ganzzahlig oder in wissenschaftlicher Notation, wenn die Anzahl der Tochterelemente 4 übersteigt (MapleV4-Bug bei der Verarbeitung von Dezimalzahlen).
Aber es läßt sich mit Maple mehr machen, als lange Formeln zu produzieren. Wir können bei dieser Gelegenheit die algebraische Behandlung von DG-systemen untersuchen (1. Ordnung, linear mit konst. Koeff.), weil dies ein wichtiges Hilfsmittel für die Lösung von DGn höherer Ordnung ist. Ein solches (homogenes) System hat immer die Form y' = M y , wobei M eine Matrix ist und y' und y Vektoren. Wäre M ein Skalar, so könnten wir die Lösung auch ohne Maple sofort hinschreiben, nämlich y = y(0) exp( M t ). Aber es ist ja denkbar, daß es bestimmte Vektoren y0 und Skalare k gibt, für die gilt:
M y0 = k y0 . Versuchen wir es am übersichtlichen Beispiel von zwei Gleichungen (zwei radioaktiven Substanzen).
| > | with(linalg): |
| > | ka:='ka':kb:='kb': |
| > | M:=matrix(2,2,[-ka,0,ka,-kb]); |
![M := matrix([[-ka, 0], [ka, -kb]])](mld1g1/mld1g1_1021.gif)
Wenn obige Gleichung gelten soll, dann muß die Determinante von
| > | Md:=matrix(2,2,[-ka-k,0,ka,-kb-k]); |
![Md := matrix([[-ka-k, 0], [ka, -kb-k]])](mld1g1/mld1g1_1022.gif)
verschwinden:
| > | det(Md); |
![]()
Die Nullstellen dieses charakteristischen Polynoms
| > | charpoly(M,k); |
![]()
sind die Eigenwerte von M:
| > | eigenvals(M); |
![]()
Wir benötigen noch die passenden Vektoren ( y0 = ( y1 , y2 )) zu den beiden Eigenwerten
| > | with(student): # fuer equate |
| > | sys:=equate(evalm(M&*[y1,y2]),evalm(-ka*[y1,y2])); |
![]()
| > | solve(sys,{y1,y2}); |
![]()
| > | sys:=equate(evalm(M&*[y1,y2]),evalm(-kb*[y1,y2]));solve(sys,{y1,y2}); |
![]()
![]()
Aber es genügt ein einziger Maple-Befehl:
| > | eigenvects(M); |
![]()
| > |
Dabei steht an erster Stelle der Eigenwert, dann seine Vielfachheit und in {} der Eigenvektor. Nun können wir unser DG-System also einfacher schreiben: y0' = k y0 mit k = -ka oder -kb und den zugehörigen Eigenvektoren y0 . Damit diese Eigenvektoren das DG-System lösen, müssen sie die Form haben: y0 = ( y1 , y2 ) exp( k t ). Damit löst aber auch jede Linearkombination der beiden Lösungen das System, insbes. erhält man nach Multiplikation obiger Vektoren mit
ka /( kb - ka ) A(0) die schon mit dsolve erzeugte Lösung A(t) und B(t).
Die Rolle der Exponentialfunktion
Wir haben bisher die Proportionalität der Exponentialfunktion zu ihrer eigenen Ableitung rein formal verwendet. Aber es gibt einen elementaren Zugang zu diesem Sachverhalt. Zu diesem Zweck gehen wir einen Schritt "zurück", nämlich von der Differential- zur Differenzengleichung. Dann wird aus y' Dy/Dt = (y(t+Dt)-y(t))/Dt und wenn wir das Zeitintervall 1 wählen können wir die aufeinanderfolgenden y -Werte numerieren:
| > | dg:=y(n+1)-y(n)=k*y(n); |
![]()
Diese rekursive Beziehung hat bekanntlich die Lösung
| > | sol:=rsolve(dg,y); |
![]()
also eine geometrische Folge mit q = 1 + k . Wir können zu beliebiger Basis q Punktplots dieser Folgen erstellen, auch zu negativer Basis. Dann wird Wachstum und Zerfall gemischt und wir bekommen Schwingungen -- gedämpfte, anwachsende und für q = -1 etwas, was wie eine Sinusschwingung aussieht. Und das obwohl wir "nur" eine DG / Differenzengl. 1. Ordnung haben! Setzen Sie also für den nächsten Plot verschiedene q ein, auch negative:
| > | q:=4/5: |
| > | plot([seq([n,q^n],n=0..10)],style=point,color=red); |
![[Maple Plot]](mld1g1/mld1g1_1033.gif)
Aber warum ist der Plot-Befehl so umständlich formuliert? Weil Maple für
| > | n:='n': |
| > | plot((-1)^n,n=0..10); |
![[Maple Plot]](mld1g1/mld1g1_1034.gif)
| > |
nur ein leeres Koordinatensystem zeigt. Woran liegt das?
Maple versucht z.B. auch
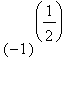 zu berechnen und das ist nicht mehr reell. Also hilft wohl
zu berechnen und das ist nicht mehr reell. Also hilft wohl
| > | plot(Re((-1)^n),n=0..10); |
![[Maple Plot]](mld1g1/mld1g1_1036.gif)
| > |
Mit evalc können wir Maple in die Karten schauen:
| > | q:='q': |
| > | evalc(q^t); |
![]()
Aber es gilt ja
| > | 'exp(Pi*I)'=exp(Pi*I); |
![]()
Man muß es nur rückwärts lesen. Negative Basis bedeutet also im allgemeinen Fall ein komplexes Argument der Exponentialfunktion ( q < 0):
| > | 'q^t'='(-abs(q))^t','exp(Pi*I*t)*exp(ln(abs(q))*t)'='exp((Pi*I+ln(abs(q)))*t)'; |
![]()
| > |
Wenn wir nun von der Differenzengleichung und der geometrischen Folge zur DG y' = k y zurückkehren, bedeutet das komplexe Eigenwerte k . Ist das nur eine Spielerei? Nein, diese Zusammenhänge reichen bis in die Quantenphysik: würde man bei reellen Exponenten (Eigenwerten) bleiben, käme man nie vom Zerfall / Wachstum zur Schwingung, nicht von der aperiodischen und inkohärenten Diffusion zur periodischen und kohärenten Welle und auch nicht zur Schrödingergleichung, die ja in der Zeit eine DG 1.Ordng. ist. Die "imaginäre Einheit" scheint eine tiefer liegende Wirklichkeit zu beschreiben ... [vgl. Reihenentwicklung von exp()]
Bei dieser Gelegenheit können wir noch die Exponentialfunktion mit komplexem Argument darstellen
| > | q:=-4/5: |
| > | rq:=evalc(Re(q^t)):iq:=evalc(Im(q^t)):aq:=evalc(abs(q^t)): #beschleunigt den Plot |
| > | plot({rq,iq,aq},t=0..5); |
![[Maple Plot]](mld1g1/mld1g1_1040.gif)
| > |
| > | spacecurve([t,rq,iq],t=0..5,axes=normal); |
![[Maple Plot]](mld1g1/mld1g1_1041.gif)
| > |
| > | sol:=dsolve({diff(y(t),t)=y(t)*k+a0},y(t),method=laplace); |
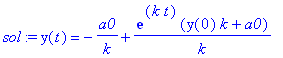
Ihr entspricht die Differenzengleichung für die geometrische Reihe (für
![]() ):
):
| > | q:='q':a0:='a0': |
| > | rsolve(s(n+1)=q*s(n)+a0,s); |
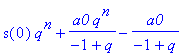
Die Lösungen können Sie wie bei den obigen Funktionen leicht darstellen (incl. q < 0 und komplexem k ).
Hier noch ein kleiner Trick zur Darstellung des s(n+1)-s(n) -Diagramms:
Differenzengleichung als Funktion geschrieben
| > | f := sn -> a0+q*sn; |
![]()
| > | fn := (sn,n) -> (f@@n)(sn) ; |
![]()
Polygonzug zur Darstellung der Iteration
| > | j:='j': a:='a': c:='c': |
| > | stufe:=(a,c)->[[c(a,j),c(a,j)],[c(a,j),c(a,j+1)],[c(a,j+1),c(a,j+1)]]; |
![]()
| > | n:='n': s0:='s0': |
| > | treppe:=stufe(s0,fn) $ j=0..n; |
![]()
| > | n:=20:q:=-4/5: |
| > | a0:=5: s0:=0: |
| > | plot({treppe,sn,f(sn)},sn=0..5,color=red); |
![[Maple Plot]](mld1g1/mld1g1_1049.gif)
| > |
Stimmt der Grenzwert (mit der Maus im Plot ausmessen)?
| > | evalf(a0/(q-1)); |
![]()
| > |
komma@oe.uni-tuebingen.de