mld2g1_10.html

mld2g1_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel A.2.2

Worksheet mld2g1_10.mws

>

c ITP Bonn Moderne Physik mit Maple 1995 filename: mld2g1

Autor: Komma Datum: 31.7.94

Lineare Differentialgleichung zweiter Ordnung

[Differentialgleichung, Differentialgleichungssystem, Schwingung, aperiodischer Grenzfall, Dämpfung, linsolve, dsolve, eigenvals, eigenvects, laplace, matrix, lineare Differentialgleichung zweiter Ordnung]

Für die "Schwingungsgleichung" (ohne Dämpfung) bekommt man drei Varianten der Lösung angeboten, je nachdem, wie man sie schreibt und ob man die Option <laplace verwendet (Maple scheint intern Annahmen über das Vorzeichen von k zu machen):

> restart; with(DEtools):with(plots):

> dg:=diff(y(t),t$2)+k*y(t)=0;

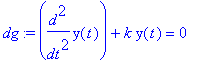
> sol:=dsolve(dg,y(t));

> dg:=diff(y(t),t$2)=-k*y(t);

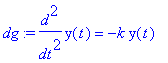
> sol:=dsolve(dg,y(t),method=laplace);

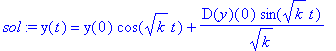
> convert(%,exp);

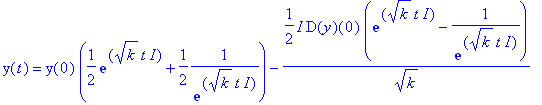
> dg:=diff(y(t),t$2)=k*y(t);

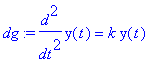
> sol:=dsolve(dg,y(t),method=laplace);

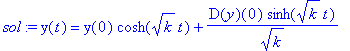
> #convert(%,exp);

Wie bereits erwähnt, kann die DG zweiter Ordnung in ein System 1.Ordnung überführt werden. Wir setzen y1=y und y2=y1', dann gilt::

> sys:=diff(y1(t),t)=y2(t),

> diff(y2(t),t)=-k*y1(t);

> dsolve({sys},{y1(t),y2(t)});

${y1(t) = _C1*sin(k^(1/2)*t)+_C2*cos(k^(1/2)*t), y2(t) = -k^(1/2)*(-_C1*cos(k^(1/2)*t)+_C2*sin(k^(1/2)*t))}$

Die Berechnung der Lösung des Systems dauert etwas länger und die Lösungen werden nicht immer in gleicher Reihenfolge angegeben. Außerdem erscheint noch ein Faktor . Alles Dinge, die vom "internen Zustand" von Maple abhängen insbes. davon, wieviel Speicher vorher schon verbraucht wurde. Aber diese kleinen "Instabilitäten" sind hier nicht so wichtig, wir wollen uns vielmehr wieder die Eigenwerte und -vektoren ansehen:

> with(linalg):

> M:=matrix(2,2,[0,1,-k,0]);

> eigenvects(M);

$[(-k)^(1/2), 1, {vector([1, (-k)^(1/2)])}], [-(-k)^(1/2), 1, {vector([1, -(-k)^(1/2)])}]$

>

Man kann sich die Eigenvektoren auch hier wieder von Hand berechnen. Diesmal mit dem Befehl <linsolve, das erspart das Aufstellen eines Gleichungssystems mit <equate:

> ew:=eigenvals(M);

> ME:=matrix(2,2,[0-ew[1],1,-k,0-ew[1]]);

> linsolve(ME,[0,0]);

>

Bevor wir zur graphischen Darstellung der Lösung übergehen, nehmen wir noch die Dämpfung hinzu und untersuchen also die allgemeine lineare (homogene) DG 2.Ordnung mit konstanten Koeffizienten.

> dg:=diff(y(t),t$2)+p*diff(y(t),t)+q*y(t)=0;

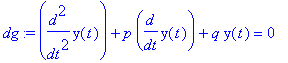
> sol:=dsolve(dg,y(t));

Oder mit der Option laplace

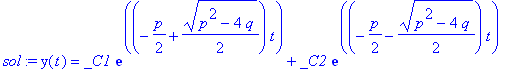
> dg:=diff(y(t),t$2)+p*diff(y(t),t)+q*y(t)=0;

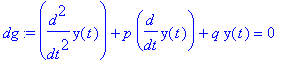
> sol:=dsolve(dg,y(t),method=laplace);

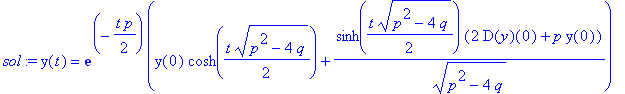
Lösung des Systems

> sys:=diff(y1(t),t)= y2(t),

> diff(y2(t),t)=-q*y1(t) - p*y2(t);

> dsolve({sys},{y1(t),y2(t)});

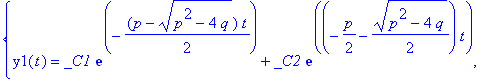
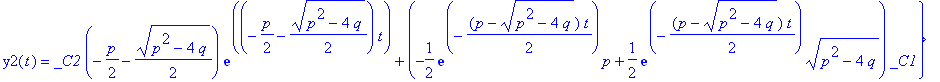
${y1(t) = _C1*exp(-1/2*(p-(p^2-4*q)^(1/2))*t)+_C2*exp((-1/2*p-1/2*(p^2-4*q)^(1/2))*t), y2(t) = _C2*(-1/2*p-1/2*(p^2-4*q)^(1/2))*exp((-1/2*p-1/2*(p^2-4*q)^(1/2))*t)+(-1/2*exp(-1/2*(p-(p^2-4*q)^(1/2))*t)*...$
${y1(t) = _C1*exp(-1/2*(p-(p^2-4*q)^(1/2))*t)+_C2*exp((-1/2*p-1/2*(p^2-4*q)^(1/2))*t), y2(t) = _C2*(-1/2*p-1/2*(p^2-4*q)^(1/2))*exp((-1/2*p-1/2*(p^2-4*q)^(1/2))*t)+(-1/2*exp(-1/2*(p-(p^2-4*q)^(1/2))*t)*...$

Wir haben nun die zwei Parameter für die "Dämpfung" und die "rückstellende Kraft" und wollen untersuchen, wie sich die Lösung mit diesen Parametern ändert. Dazu besorgen wir uns die Koeffizienten von t in der Exponentialfunktion, also die Eigenwerte:

> q:='q':p:='p':

> M:=matrix(2,2,[0,1,-q,-p]);

> ew:=eigenvals(M);

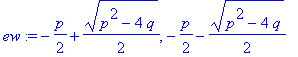
Schwingung tritt nur ein, wenn der Radikand negativ ist, also für:

>

> simplify(isolate(p^2-4*q<0,p));

>

Das hat man natürlich auch schnell im Kopf gerechnet - die letzten beiden Befehle sollten nur eine kleine Demonstration zum Umgang mit Ungleichungen sein. Viel aussagekräftiger sind aber Plots, d.h. wir stellen den Imaginärteil und Realteil der Eigenwerte dar. Die folgende Abkürzung beschleunigt den Plot (vor allem bei der 3d-Darstellung):

> ie1:=evalc(Im(ew[1])):ie2:=evalc(Im(ew[2])):

> re1:=evalc(Re(ew[1])):re2:=evalc(Re(ew[2])):

Wir halten zunächst q fest und variieren p:

> p:='p':q:=1:

> p1:=plot({ie1,ie2},p=-5..5,scaling=constrained): p1;

> p2:=plot({re1,re2},p=-5..5,scaling=constrained): p2;

> display({p1,p2});

Dem Plot kann man für q>0 schon alle Typen der Bewegung entnehmen: Im Bereich der Ellipse (konjugiert komplexe Eigenwerte) liegt eine exponentiell gedämpfte oder anwachsende Schwingung vor, mit einer Frequenz, die immer kleiner ist als im ungedämpften Fall. Für p=+-2*sqrt(q) wird die Frequenz Null, wir haben den aperiodischen Grenzfall mit nur einem Eigenwert. Es schließt sich für positive p die aperiodische Kriechbewegung an und für negative p exponentielles Wachstum, wobei für betragsmäßig große p die Hyperbeln durch ihre Asymptoten ersetzt werden können, also die Eigenwerte 0 oder -p.

Den vollständigen Überblick über die Änderung der Eigenwerte mit p und q kann man sich mit 3d-Plots verschaffen:

> p:='p':q:='q':

> pim:=plot3d({ie1,ie2},p=-5..5,q=-1..5,axes=boxed,color=red): pim;

> pre:=plot3d({re1,re2},p=-5..5,q=-1..5,axes=boxed,color=blue,style=line): pre;

> display({pim,pre});

Es lohnt sich, den aperiodischen Grenzfall (p=2*sqrt(q)) näher zu untersuchen, denn hier müßte ein zweifacher Eigenwert auftauchen:

> dg:=diff(y(t),t$2)+2*sqrt(q)*diff(y(t),t)+q*y(t)=0;

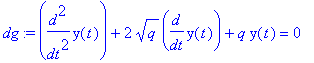
> sol:=dsolve(dg,y(t));

Also mit k=sqrt(q)

> p:='p':q:='q':

> dgr:=diff(y(t),t$2)+2*k*diff(y(t),t)+k^2*y(t)=0;

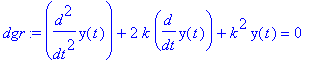
> solgr:=dsolve(dgr,y(t),method=laplace);

Für den zweifachen Eigenwert kommt also die partikuläre Lösung t*exp(-k*t) hinzu

> M:=matrix(2,2,[0,1,-k^2,-2*k]);

> eigenvects(M);

Für die Darstellung der Bewegung eignet sich am besten die mit der Laplace-Methode erzeugte Lösung, weil sie die Anfangsbedingungen enthält und deshalb am leichtesten zu interpretieren ist.

> p:='p':q:='q':y(0):='y(0)': D(y)(0):='D(y)(0)':

> dg:=diff(y(t),t$2)+p*diff(y(t),t)+q*y(t)=0:

> sol:=dsolve(dg,y(t),method=laplace);

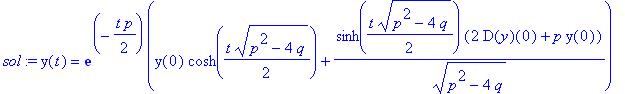
Wir können wieder versuchen, ein Maximum an Information zu erhalten, indem wir nicht nur eine bestimmte Bewegung darstellen, sondern z.B. den Parameter p ebenfalls verändern. (Falls Sie sich über den Laufbereich von p wundern: mit obiger Lösung läßt Maple u.U. eine Lücke beim aperiodischen Grenzfall -- z.B. für p=0..3.)

> y(0):=5: D(y)(0):=-2:

> p:='p': q:=1:

> plot3d(rhs(sol),t=0..10,p=0..3.1,axes=boxed);

> #plot3d(evalc(Re(rhs(sol))),t=0..10,p=0..3.1,axes=boxed);

>

Den Übergang von periodischer Bewegung zu aperiodischer Bewegung kann man noch besser darstellen, wenn man im 3d-Plot Höhenlinien wählt, oder einen Konturplot macht:

In Maple10 evalc(Re(...))) erforderlich

> contourplot(evalc(Re(rhs(sol))),t=0..10,p=0..4.1,axes=boxed,numpoints=1000);

Man sieht hier wieder die Abnahme der Frequenz mit wachsender Dämpfung (p), aber auch -- und das ist für die praktische Anwendung wichtig -- daß ein schwingungsfähiges System am schnellsten zur Ruhe kommt, wenn man p=2*sqrt(q) wählt (Meßgeräte, Stoßdämpfer ... war da nicht noch etwas mit dem Tunneleffekt?).

>

komma@oe.uni-tuebingen.de