Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel A.2.2
Worksheet mld2g2_10.mws
| > |
c ITP Bonn 1995 Moderne Physik mit Maple filename: mld2g2
Autor: Komma Datum: 3.8.94
Lineare DG. 2.Ordnung (Forts.)
[Differentialgleichung, Richtungsfeld, Phasenportrait, Phasengleichung, Reduktion, komplexe Eigenwerte, Schwingungsgleichung, Differenzengleichung,Vieta, Fibonacci, Laplacetransformation, homogene DG, inhomogene DG, partikuläre Lösung, Resonanzkurve], [rsolve, dsolve, dfieldplot, phaseportrait, laplace], [lineare Differentialgleichung zweiter Ordnung]
Natürlich darf das Richtungsfeld und das Phasenportrait nicht fehlen. Man erzeugt beides am bequemsten mit der Matrix M des zugehörigen Systems erster Ordnung.
| > | restart; with(DEtools):with(plots):with(linalg): |
| > | q:='q':p:='p': |
| > | #M:=matrix(2,2,[0,1,-q,-p]); |
#q:=1:p:=1/4:
| > | #df:=dfieldplot(M,[y1,y2],t=-1..1,y1=-2..2,scaling=constrained): |
| > | #ph:=phaseportrait(M,[a,b],t=0..10,{seq([0,i/2,0],i=-2..2)},stepsize=.2): |
| > |
dfieldplot und phaseportrait mit der Matrix nicht mehr möglich.
| > |
| > |
Alternative Formulierung (man beachte die eckigen Klammern um [sys] in phaseportrait):
| > | p:='p': q:='q': |
| > | sys:=diff(y1(t),t)= y2(t), |
| > |
| > | diff(y2(t),t)=-q*y1(t) - p*y2(t); |
![]()
| > | q:=1:p:=1: |
| > | phaseportrait([sys],[y1,y2],t=0..10,{[0,1,0],[0,-1,0]},stepsize=.2); |
![[Maple Plot]](mld2g2/mld2g2_102.gif)
| > |
Man kann die Phasengleichung auch selbst aufstellen, indem man die Zeit aus den beiden Gleichungen eliminiert (dy2/dy1=dy2/dt*dt/dy1). Das führt auf die autonome (skleronome) DG 1.Ordnung.
| > | p:='p': q:='q': |
| > | pg:=diff(y2(y1),y1)=-p-q*y1/y2(y1); |
![]()
Allerdings haben nun die Pfeile in der unteren Hälfte des Richtungsfeldes die falsche Richtung:
| > | q:=1: p:=1/4: |
| > | dfieldplot(pg,y2(y1),y1=-1..1,y2=-1..1,scaling=constrained); |
![[Maple Plot]](mld2g2/mld2g2_104.gif)
| > |
Früher (vor CAS) mußte man die Phasengleichung so aufstellen -- und hatte dann noch nicht einmal die Lösung. Mit Maple sieht man wenigstens, daß die Lösung der Phasengleichung nicht ganz einfach ist ... (sie wird wieder wie die logarithmische Spirale implizit mit einem überflüssigen y1 angegeben). Vielleicht wollen Sie damit weiterarbeiten?
| > | q:='q': p:='p': |
| > | sol:=dsolve(pg,y2(y1)); |
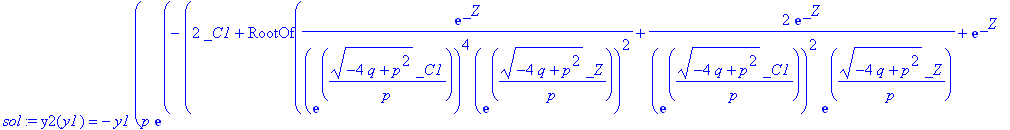
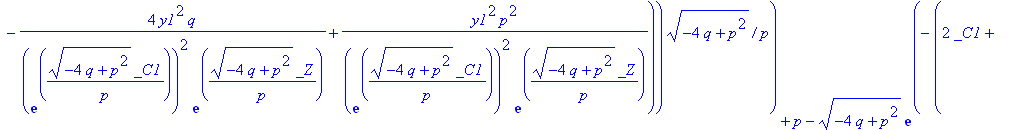


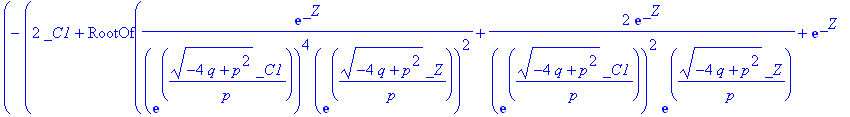

| > |
In Vor-CAS-Zeiten war noch eine weitere Lösungsmethode beliebt, nämlich die Reduktion der Ordung einer DG. Wir wollen die Reduktion hier kurz streifen, nicht als Lösungsmethode sondern zum Vergleich mit der DG 1.Ordnung. Für die lineare DG mit konstanten Koeffizienten hat die Lösung ja die Eigenschaft y''=k*y'=k^2*y, wenn man nur einen Eigenwert verwendet, der im allgemeinen Fall aber komplex ist. Damit läßt sich y' oder y'' eliminieren. Wir versuchen es mit der Eliminierung von y'':
| > | dg:=k^2*y(t)+p*diff(y(t),t)+q*y(t)=0; |
![]()
| > | sol:=dsolve(dg,y(t)); |

Probe:
| > | ew:=eigenvals(M); |
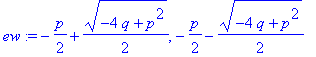
| > | assign(sol): |
| > | simplify(subs(k=ew[1],y(t))); |
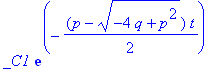
Bitte nachrechnen! (Am einfachsten mit dem charakteristischen Polynom)
Die DG 1.Ordng.
| > | y(t):='y(t)': |
| > | diff(y(t),t)=k*y(t); |
![]()
mit dem (ggf.) komplexen Koeffizienten (EW)
| > | 'k'=ew; |

ist also gleichwertig mit "der Schwingungsgleichung" und man sieht jetzt auch den Zusammenhang zwischen Re(k), Im(k) und p und q.
Wir wollen nun -- wie schon bei der DG 1.Ordng. -- mit der Differenzengleichung vergleichen. Das ist diesmal die verallgemeinerte Fibonacci-Gleichung:
| > | gl:=y(n+2)+p*y(n+1)+q*y(n)=0; |
![]()
Mit der Lösung
| > | sol:=rsolve(gl,y); |
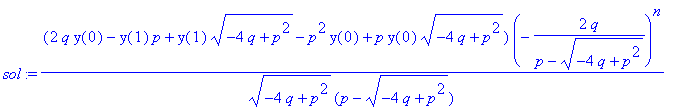
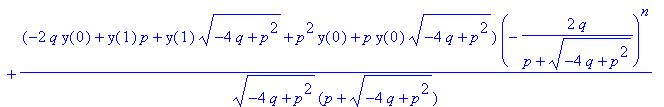
Das ist die Linearkombination zweier geometrischer Folgen mit den Eigenwerten als Basen. So sieht man es besser:
| > | y(0):=0: y(1):=1: |
| > | simplify(sol); |
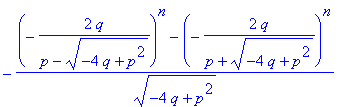
Und nach Vieta gilt:
| > | ew[1]*ew[2]=expand(ew[1]*ew[2]); |
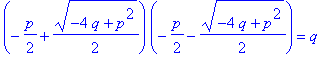
Wie sieht die Lösung der Fibonacci-Gleichung aus?
| > | isol:=evalc(Im(sol)): rsol:=evalc(Re(sol)): asol:=evalc(abs(sol)): |
| > | q:=-2: p:=-0.1: |
| > | plot({rsol,isol,asol},n=0..20); |
![[Maple Plot]](mld2g2/mld2g2_1022.gif)
Das ist eine Anregung, die Fibonacci-Gleichung mit Maple ein wenig zu erforschen ... man kann sich schlecht gegen die Eigendynamik dieses CASs wehren. Der 3d-Plot liefert je nach dem Wert von p wieder gedämpfte Schwingungen unterschiedlicher Frequenz
| > | q:=1/2: p:='p': |
| > | plot3d(asol,n=0..10,p=-1..1,axes=boxed); |
![[Maple Plot]](mld2g2/mld2g2_1023.gif)
Im Unterschied zur Differentialgleichung steht aber in der Lösung der Differenzengleichung der Logarithmus der Eigenwerte in der Exponentialfunktion (wenn man zur Basis e übergeht) und das hat beträchtliche Auswirkungen auf die Bewegung (Lösung):
| > | p:='p': |
| > | q:=2: |
| > | plot({Im(ln(ew[1])),Im(ln(ew[2])),Re(ln(ew[1])),Re(ln(ew[2]))},p=-5..5); |
![[Maple Plot]](mld2g2/mld2g2_1024.gif)
| > |
Für -2*sqrt(q)<p<2*sqrt(q) bekommt man wieder Schwingungen aber mit einer Frequenz, die Pi nicht überschreitet und die "Dämpfung" ist ln(abs(q)) (wieder mit Vieta ist mit den konjugiert komplexen Eigenwerten das Betragsquadrat eines Eigenwertes q). Dort wo bei der DG der aperiodische Grenzfall lag, beginnt nun ein Gebiet, in dem mit wachsendem p eine "gedämpfte" Schwingung mit der festen Freqenz Pi stattfindet. Nur für p<-2*sqrt(q) stimmt der Charakter der Lösungen von DG und Differenzengleichung insofern überein, daß keine Schwingung möglich ist, aber bei der Differenzengleichung ist immer noch exponentielle Abnahme möglich. Mit den folgenden Plots können Sie diese Zusammenhänge weiter untersuchen.
| > |
| > | q:='q': |
| > | p:=2: |
| > | plot({Im(ln(ew[1])),Im(ln(ew[2])),Re(ln(ew[1])),Re(ln(ew[2]))},q=-5..5,-5..5); |
![[Maple Plot]](mld2g2/mld2g2_1025.gif)
Weitere Darstellungsmöglichkeiten
| > | q:='q': p:='p': |
| > | p1:=plot3d({Re(ln(ew[1])),Re(ln(ew[2]))},p=-5..5,q=0.1..5,axes=boxed,view=-2..5): |
| > | p2:=plot3d({Im(ln(ew[1])),Im(ln(ew[2]))},p=-5..5,q=-5..5,axes=boxed,view=-2..5): |
| > | #p1; |
| > | display({p1,p2}); |
![[Maple Plot]](mld2g2/mld2g2_1026.gif)
| > |
| > | q:=1/4: p:='p': |
| > | plot({seq(Im(ew[1]^n),p=-1..1)},n=0..10); |
![[Maple Plot]](mld2g2/mld2g2_1027.gif)
| > |
| > | q:=1/2:p:='p': |
| > | plot3d(Re(ew[1]^n),p=-1.5..2,n=0..10,axes=boxed); |
![[Maple Plot]](mld2g2/mld2g2_1028.gif)
Es bleiben noch zwei Themen, die Physiker besonders interessieren, wenn sie es mit "der Schwingungsgleichung" zu tun haben: die Laplace-Transformation und der Umgang mit partikulären Lösungen bzw. die Rolle der Inhomogenität.
| > | with(inttrans): |
Wir können die nun schon so oft verwendete Laplace-Option am Beispiel der inhomogenen DG 2.Ordnung erläutern.
Mit Hilfe der Laplace-Transformation
| > | F(s)=Int(exp(-s*t)*f(t),t=0..infinity); |
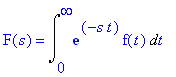
lassen sich Differentialgleichungen algebraisieren. Das liegt an folgender Eigenschaft der Laplace-Transformation:
| > | laplace(diff(f(t),t),t,s); |
![]()
D.h. die Laplace-Transformierte der Ableitung einer Funktion ist im wesentlichen die Laplace-Transformierte der Funktion mal s. Dies führt zu:
| > | q:='q': p:='p':y:='y':Y:='Y':r:='r': |
| > | ladg:=laplace(diff(y(t),t$2)+p*diff(y(t),t)+q*y(t)=r(t),t,s); |
![]()
Die Ableitungen sind verschwunden und wir können zur besseren Handhabung der Transformierten einen Namen geben:
| > | subs(laplace(y(t),t,s)=Y,ladg); |
![]()
Die Transformierte Y ist gesucht, also:
| > | Y:=solve(%,Y); |
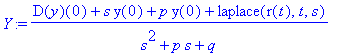
Wir machen zunächst die Probe für die homogene DG:
| > | r(t):=0: Y; |
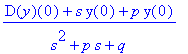
Nun benötigen wir noch die Rücktransformierte:
| > | invlaplace(Y,s,t); |
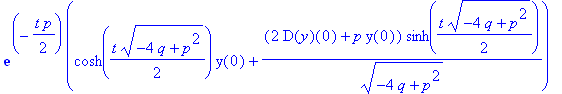
Das läuft also hinter den Kulissen ab, wenn wir die Option <laplace angeben.
Der wichtigste Fall der inhomogenen DG ist die erzwungene Schwingung:
| > | r(t):=A*sin(omega*t); |
![]()
| > | Y; |
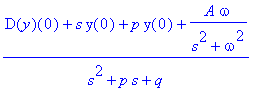
| > | z:=simplify(invlaplace(Y,s,t)); |
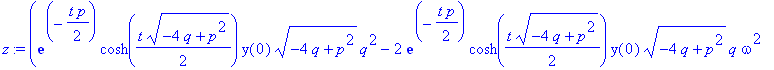
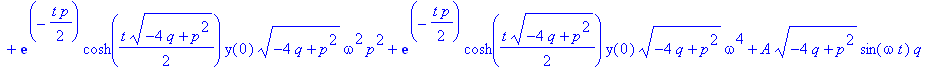
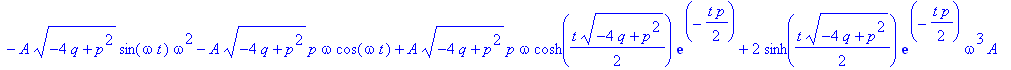


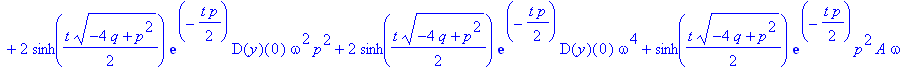

| > | y(0):=0: z; |
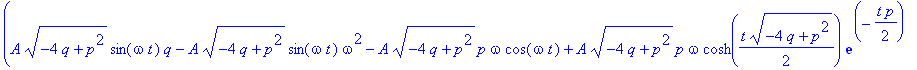
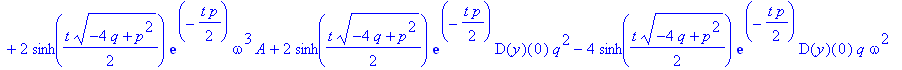
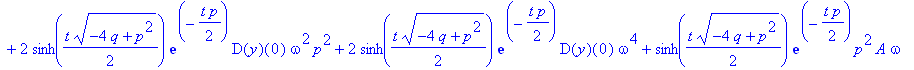
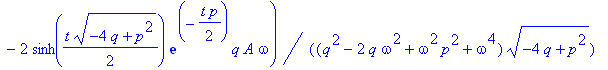
Vergleichen Sie dies mit der Lösung, die dsolve liefert.
Wir kommen zum letzten Thema dieses Worksheets:
Wenn wir uns mehr für die Struktur der Lösung interessieren, können wir auch so vorgehen.
| > | restart: |
| > | dglh:=diff(diff(y(t),t),t)+p*diff(y(t),t)+q*y(t)=0; |
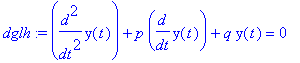
Inhomogene DG:
| > | r:='r': |
| > | dgli:=diff(diff(y(t),t),t)+p*diff(y(t),t)+q*y(t)=r(t); |
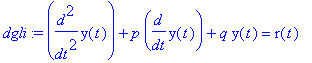
Lösung der homogenen DG:
| > | solh:=rhs(dsolve(dglh,y(t))); |
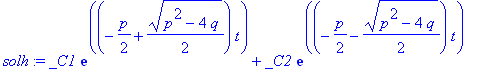
| > |
Lösung der inhomogenen DG:
| > | soli:=rhs(dsolve(dgli,y(t))); |
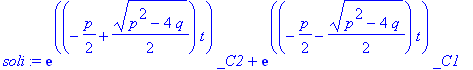
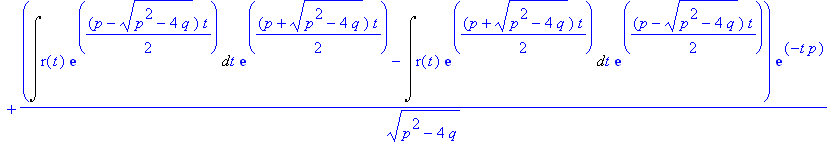
In der allgemeinen Lösung sind u.U. die Integrationskonstanten _C1 und _C2 vertauscht.
| > | solh:=subs(_C1=c1,_C2=c2,solh); |
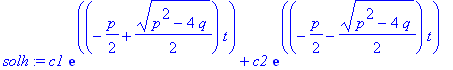
| > | soli:=subs(_C1=c2,_C2=c1,soli); |
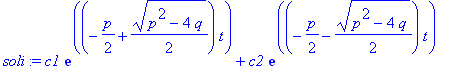

| > | solp:=soli-solh; |

| > |
Die allgemeine Lösung soli besteht aus Integralen, die von der Störfunktion abhängen + Termen der
Eigenschwingung (mit den Integrationskonstanten _C1 und _C2). Nach dem Einschwingen sollte also die Störfunktion die Bewegung bestimmen.
Wir wählen z.B. eine sinusförmige Erregung:
| > | r(t):=A*exp(I*Omega*t); |
![]()
| > | solp:=value(solp); |
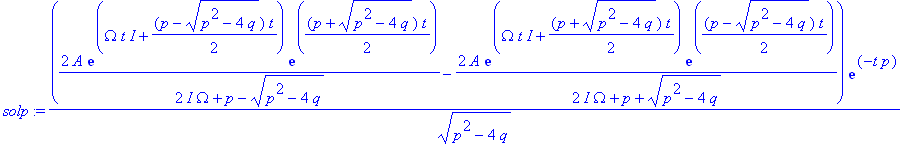
| > |
Es sollte aber eine Bewegung mit Omega herauskommen!?
| > |
| > | solp:=simplify(solp); |
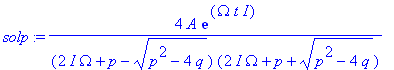
| > |
| > | simplify(solp,radical,symbolic); |

| > |
| > |
| > | expand((2*I*Omega+p+sqrt(p^2-4*q))*(2*I*Omega+p-sqrt(p^2-4*q))); |
![]()
| > | solp:=simplify(numer(solp)/expand(denom(solp))); |
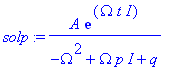
| > |
| > |
Welche Amplitude hat sie?
| > |
| > | asolp:=simplify(evalc(abs(solp))); |
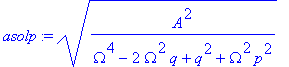
| > |
Das sieht doch nach Resonanz aus?
| > | with(student): |
| > | ampl:=completesquare(asolp,q); |
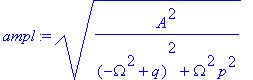
Und die Phase?
| > | t:=0: |
| > | phase:=evalc(Im(solp)/Re(solp)); |

arctan(phase) springt, arctan(Im,Re) bleibt auf Hauptwert
| > | A:=20: p:=1: q:=30: |
| > | plot({ampl,-arctan(Im(solp),Re(solp))},Omega=0..10); |
![[Maple Plot]](mld2g2/mld2g2_1067.gif)
| > |
| > |
komma@oe.uni-tuebingen.de