PDF-Buch   Moderne Physik mit Maple

Update auf Maple 10

Kapitel 3.2.1

Worksheet paket_10.mws

>

>

c International Thomson Publishing Bonn  1995        filename: paket1

Autor: Komma                                                         Datum: 20.8.94                         

Thema: Wellenpakete

In Maple 6 nicht stabil: Die Reihenfolge der ops und das Rücksetzen der Annahmen sind eine reines Lotteriespiel insbes. mit %

Linearkombinationen von Lösungen einer linearen DG sind wieder Lösungen, d.h. Lösungen können superponiert werden.

Eine Lösung ist die ebene Welle

>

>	restart;with(inttrans);

>	yk:=(x,t)->exp(I*(k*x-omega*t));

die z.B. mit dem Gewicht

>	wk:=exp(-((k-k0)^2)/(2*sk^2));

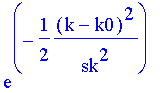
auftritt. Im Falle des kontinuierlichen Spektrums muß also

>	z:=(x,t)->wk*yk(x,t):

>

z(x,t);

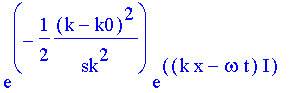
über alle Wellenzahlen integriert werden. Wenn wir den Zusammenhang von omega und k noch offen halten wollen, können wir das zunächst für t=0 tun:

>	assume(sk>0): # sk koennte komplex sein

>	int(z(x,0),k=-infinity..infinity);

>

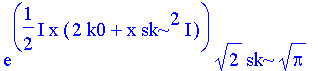
Diese Integration ist aber nichts anderes als eine Fouriertransformation (hier invers wegen +kx und geeign. normiert)

>	omega:='omega':

>	pak0:=invfourier(wk,k,x)*2*Pi;

>

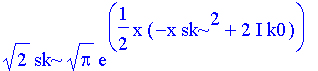
Es wird also wie bei der Schwingung eine Gaußverteilung in eine Gaußverteilung transformiert und das Produkt der Varianzen ist wieder ~1: ein gut lokalisiertes Wellenpaket kann nur durch ein breites Spektrum der Wellenzahlen aufgebaut werden. Die Frage ist nun, wie sich dieses Paket im Laufe der Zeit entwickelt. Im Falle der Wellengleichung gilt

>	omega:=k*c;

>	pakw:=int(z(x,t),k=-infinity..infinity);

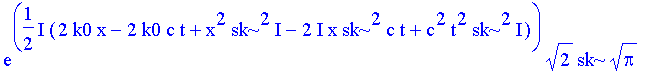
>	simplify(%);

>

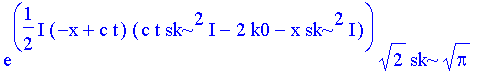
Der Exponent läßt sich vereinfachen zu:

>	collect(op(op(1,%)),sk); # nicht stabil (+/-), bitte vorher die Ausgabe lesen, bzw. auf Änderung achten.

Das ist ein Gauß-Paket, das sich mit der Geschwindigkeit c bewegt.

>	pakw:=exp(subs(sk=1/sx,%));

>	repakw:=evalc(Re(pakw)):

>

#repakw;

>	k0:=2: c:=3: sx:=4:

>

>	with(plots):

>	animate(repakw,x=-20..20,t=-10..10,frames=80,numpoints=200);

>

Aber es lohnt sich wieder, auf Vollbild zu stellen und mit den Parametern zu spielen.

(Man kann auch noch eine Blende reinprogrammieren).

>

Im Falle der sgl gilt:

>	sk:='sk': k0:='k0':b:='b':k:='k':

>	omega:=b*k^2;

>	#omega:=taylor(omega,k=k0);

>

>

>

Der Exponent des Integranden sieht also so aus:

>	expo:=op(combine(wk*yk(x,t),power));

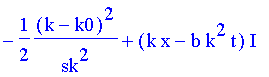
Für t=0 gilt wieder das Gleiche wie oben. Wie entwickelt sich das Paket?

>	assume(sk>0,k0>0,t>0):

>	pak:=int(z(x,t),k=-infinity..infinity);

>

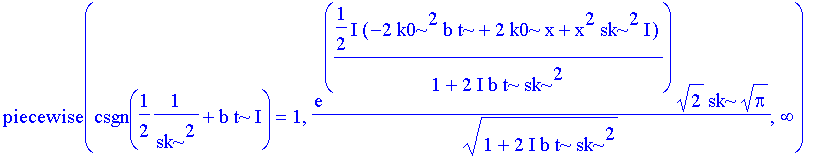
In Maple 6 ein Ergebnis!   So ist kein Ergebnis zu bekommen. Wir können aber versuchen, den Exponenten zu einem vollständigen Quadrat zu ergänzen -- so wie man das von Hand auch machen würde, weil dann die Fehlerfunktion ins Spiel gebracht werden kann.

>	with(student): b:='b':

>

expo;

>	expoc:=completesquare(expo,k); # Reihenfolge fuer op-Befehl (s.u.) beachten!

>

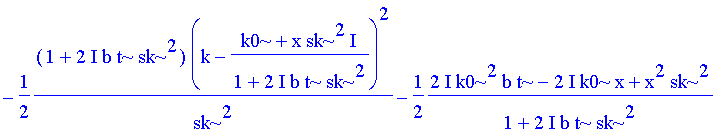
op(%);

>

Der erste Summand ist nun ein vollständiges Quadrat in k und von der Form a*(k-etwas)^2. Also setzen wir an:

>	assume(a>0):

>	paks:=int(exp(-a*(k-etwas)^2+op(2,expoc)),k=-infinity..infinity);

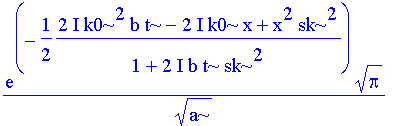
>	# bis hier her läuft es, kopie von paks:

paks := exp(-1/2*(2*I*k0^2*b*t-2*I*k0*x+x^2*sk^2)/(1+2*I*b*t*sk^2))*sqrt(Pi)/(sqrt(a));

>

>

>

"Etwas" ist verschwunden und wir benötigen noch a.

>	op(op(1,{op(expoc)})); # nicht stabil: op(1,{}) oder op(2,{})

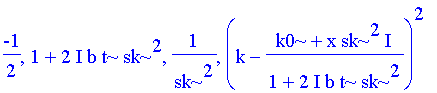
>	as:=op(1,{op(expoc)})/op(4,op(1,{op(expoc)}));

>

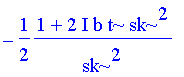
# kopie

as := -1/2*(1+2*I*b*t*sk^2)/(sk^2);

>

>

Bis man die Klammern in op(()) richtig gesetzt hat, hat man's auch von Hand nochmal geschrieben. Oder mit der Maus geholt...

>	paks:=subs(a=as, sk=s,paks);

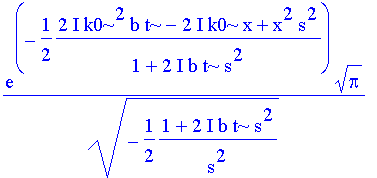
>	apaks:=simplify(evalc(abs(paks))^2);

>

>	t:='t': k0:='k0':

>	# Annahmen von Hand (C&P) entfernen:

>	apaks := 2*exp(-s^2*(2*k0*b*t-x)^2/(1+4*b^2*t^2*s^4))*Pi*csgn(conjugate(s)^2)*s^2/(sqrt(1+4*b^2*t^2*s^4));

>

>

>

>	with(plots): # es dauert wieder ...

>	s:=2: b:=3: k0:=4:t:='t':

>	animate(apaks,x=-40..40,t=-1..1,frames=25,numpoints=200);

>

Die folgenden Befehle sollen die Animation des Realteils beschleunigen

>	repaks:=simplify(evalc(Re(paks))); # auch diese "simple" Umformung benoetigt ihre Zeit

>	epaks:=simplify(evalf(repaks));

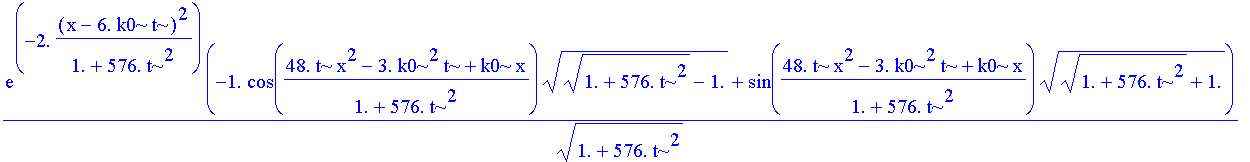
>	# Annahmen entfernen

>	epaks := 3.544907702*exp(-2.*(6.*k0*t-1.*x)^2/(1.+576.*t^2))*(cos((-48.*t*x^2+3.*k0^2*t-1.*k0*x)/(1.+576.*t^2))*sqrt(sqrt(1.+576.*t^2)-1.)+sin((-48.*t*x^2+3.*k0^2*t-1.*k0*x)/(1.+576.*t^2))*sqrt(sqrt(1.+576.*t^2)+1.))/(sqrt(1.+576.*t^2));

>

>

>

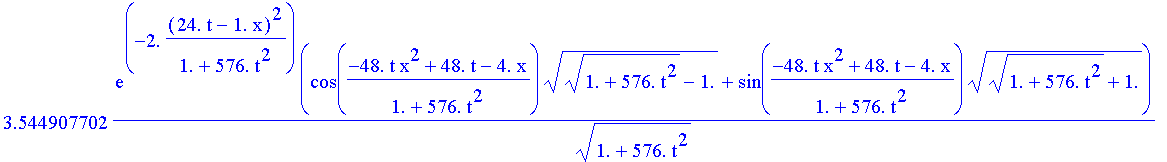
Und jetzt lohnt sich die Geduld wirklich ... es sind ja nur ein paar Minuten

(Die underflow-Fehlermeldung ist unkritisch)

>	animate(epaks,x=-20..20,t=-1..1,numpoints=200);

>

>	#csgn(-I-1);

>

#epaks;

>

>

>

Die Anteile mit kleinen Wellenlängen bewegen sich schneller als die mit großen Wellenlängen. Man spricht immer vom *Zerfließen* eines Paketes durch Dispersion, weil man darauf fixiert ist, vorauszuberechnen. Aber wenn Sie die Animation laufen lassen, *sehen* Sie, daß sich das Paket auch *bildet*. Im Gegensatz zum Wellenpaket "der Wellengleichung", dessen Bild sich wie ein starrer Körper gleichförmig bewegt, entsteht und vergeht hier Information, weil die Kohärenz fehlt.  

Dreidimensional:

>	t:='t':s:=2:

>

apaks;

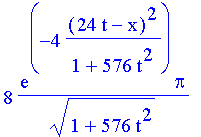
>	plot3d(apaks,x=-40..40,t=-1..1,grid=[50,50],style=hidden,axes=framed);

>

(Verwenden Sie auch den contour-style im letzten Plot.)

Die Geschwindigkeit, mit der die Information verlorengeht, hängt davon ab, wie genau man das Paket lokalisieren möchte: je geringer die Paketbreite 1/s, desto schneller das Zerfließen -- aber auch das Entstehen. Zunächst eine Momentaufnahme

>

apaks;

>	s:='s':t:=0.1:x:='x': # für x=-40..40 'exponent too large'

>	plot3d(evalf(apaks),x=-20..20,s=0.1..2,grid=[50,50],style=hidden,axes=framed);

>

>	#eval(apaks,{s=0.1,x=40});

>	#s:='s':x:=30:

>	#plot(evalf(apaks),s=0.1..2,axes=framed);

>

>

Und die Animation

>	s:='s':t:='t':

>	animate3d(apaks,x=-20..20,s=0.1..2,t=-1..1,axes=framed,style=hidden);#grid=[50,50]);

>

apaks;

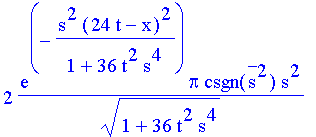
>	# auch hier wegen csgn exponent too large für frames=20 (t=0?)

Für kleine s (etwa 0.4) behält das Paket seine Form fast bei.

Anm.: Die Gruppengeschwindigkeit hängt nur von k0 ab.

Siehe auch: Schrödingers Oszillator

komma@oe.uni-tuebingen.de