propa_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 5.3.1

Worksheet propa_10.mws

c ITP Bonn 1995                filename: propa

Autor: Komma                   Datum: 9.10.94                        

Thema: Feynman - Propagator des freien Elektrons

>    restart:

Aufbau des Propagators

>    K:=f(x[1],x[0]);

K := f(x[1],x[0])

>    for i from 2 to 4 do

>    K:=Int(f(x[i],x[i-1])*K,x[i-1]):

>    od;

K := Int(f(x[2],x[1])*f(x[1],x[0]),x[1])

K := Int(f(x[3],x[2])*Int(f(x[2],x[1])*f(x[1],x[0]),x[1]),x[2])

K := Int(f(x[4],x[3])*Int(f(x[3],x[2])*Int(f(x[2],x[1])*f(x[1],x[0]),x[1]),x[2]),x[3])

>   

Als Prozedur

>    K:=proc(n) local K,i;

>    K:=f(x[1],x[0]);

>    for i from 2 to n do

>    K:=int(f(x[i],x[i-1])*K,x[i-1]=-infinity..infinity):

>    #K:=Int(f(x[i],x[i-1])*K,x[i-1]):

>    od:

>    end;

K := proc (n) local K, i; K := f(x[1],x[0]); for i from 2 to n do K := int(f(x[i],x[i-1])*K,x[i-1] = -infinity .. infinity) end do end proc

>   

Für Integration

>    assume(c<0):

>    #c:='c':

>    #value(");

>    f:=(u,v)->exp(c*(u-v)^2);

f := (u, v) -> exp(c*(u-v)^2)

Test

>    seq(K(i),i=2..5);

1/2*exp(1/2*c*(x[2]^2+x[0]^2-2*x[2]*x[0]))*2^(1/2)/(-c)^(1/2)*Pi^(1/2), -1/3*exp(1/3*c*(x[3]^2+x[0]^2-2*x[3]*x[0]))/c*Pi*3^(1/2), -1/2*exp(1/4*c*(x[4]^2+x[0]^2-2*x[4]*x[0]))/c*Pi^(3/2)/(-c)^(1/2), 1/5*...

>   

Also wäre als Normierung angebracht

>    sqrt(-c/Pi);

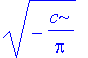
(-c/Pi)^(1/2)

>    f:=(u,v)->sqrt(-c/Pi)*exp(c*(u-v)^2);

f := (u, v) -> sqrt(-c/Pi)*exp(c*(u-v)^2)

>    seq(K(i),i=2..9);

-1/2*exp(1/2*c*(x[2]^2+x[0]^2-2*x[2]*x[0]))*c/Pi^(1/2)*2^(1/2)/(-c)^(1/2), -1/3*1/Pi^(1/2)*exp(1/3*c*(x[3]^2+x[0]^2-2*x[3]*x[0]))*c*3^(1/2)/(-c)^(1/2), -1/2*1/Pi^(1/2)*exp(1/4*c*(x[4]^2+x[0]^2-2*x[4]*x...
-1/2*exp(1/2*c*(x[2]^2+x[0]^2-2*x[2]*x[0]))*c/Pi^(1/2)*2^(1/2)/(-c)^(1/2), -1/3*1/Pi^(1/2)*exp(1/3*c*(x[3]^2+x[0]^2-2*x[3]*x[0]))*c*3^(1/2)/(-c)^(1/2), -1/2*1/Pi^(1/2)*exp(1/4*c*(x[4]^2+x[0]^2-2*x[4]*x...
-1/2*exp(1/2*c*(x[2]^2+x[0]^2-2*x[2]*x[0]))*c/Pi^(1/2)*2^(1/2)/(-c)^(1/2), -1/3*1/Pi^(1/2)*exp(1/3*c*(x[3]^2+x[0]^2-2*x[3]*x[0]))*c*3^(1/2)/(-c)^(1/2), -1/2*1/Pi^(1/2)*exp(1/4*c*(x[4]^2+x[0]^2-2*x[4]*x...

>   

K zu beliebigem n

>   

>    K(7);

1/7*1/Pi*(-c*Pi)^(1/2)*exp(1/7*c*(x[7]^2+x[0]^2-2*x[7]*x[0]))*7^(1/2)

>    Kn:=subs(7=n,K(7));

Kn := 1/7*1/Pi*(-c*Pi)^(1/2)*exp(1/7*c*(x[n]^2+x[0]^2-2*x[n]*x[0]))*n^(1/2)

>    Kn:=subs(-1/7=-1/n,Kn);

Kn := 1/7*1/Pi*(-c*Pi)^(1/2)*exp(1/7*c*(x[n]^2+x[0]^2-2*x[n]*x[0]))*n^(1/2)

>    Kn:=subs(1/7=1/n,Kn);

Kn := 1/Pi*(-c*Pi)^(1/2)*exp(c*(x[n]^2+x[0]^2-2*x[n]*x[0])/n)/n^(1/2)

>   

>   

Ersetzen der Konstanten c (siehe Buch)

>    Kn:=subs(c=I*a/epsilon,Kn);

Kn := 1/Pi*(-I*a/epsilon*Pi)^(1/2)*exp(a/epsilon*(x[n]^2+x[0]^2-2*x[n]*x[0])/n*I)/n^(1/2)

>    factor(%);

1/Pi*(-I*a/epsilon*Pi)^(1/2)*exp(a*(x[0]-x[n])^2/epsilon/n*I)/n^(1/2)

>    subs(epsilon=t/n,%);

1/Pi*(-I*a/t*n*Pi)^(1/2)*exp(a*(x[0]-x[n])^2/t*I)/n^(1/2)

>    Kn:=combine(%);

Kn := 1/Pi*(-I*a/t*n*Pi)^(1/2)*exp(a*(x[0]-x[n])^2/t*I)/n^(1/2)

>    K:=radsimp(%);

K := 1/t*(-I*a*Pi*t)^(1/2)*exp(a*(x[0]-x[n])^2/t*I)/Pi

einfachere Schreibweise

>    x[n]:=x: x[0]:=0:t:='t':a:='a':

>    K;

1/t*(-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)/Pi

Feynmans Phase (für x=0)

>    evalc((1/sqrt(I)));

1/2*2^(1/2)-1/2*I*2^(1/2)

unsere Phase (je nach Maple-Version ;-))

>    evalc((-1)^(3/4));

-1/2*2^(1/2)+1/2*I*2^(1/2)

Mit einem Unterschied von Pi. Aber wir können natürlich wie Feynman nur mit dem Betrag des Vorfaktors rechnen (quod libet iovi...)

>    Kw:=K/(-1)^(3/4);

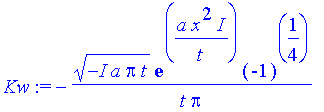
Kw := -1/t*(-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)/Pi*(-1)^(1/4)

>    assume(t>0,a>0);

>    RK:=evalc(Re(Kw));

RK := -1/t/Pi*Re((-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)*(-1)^(1/4))

>    RK:=subs(t=th,a=ah,RK):

>    t:='t':a:='a':

>    RK:=subs(th=t,ah=a,RK);

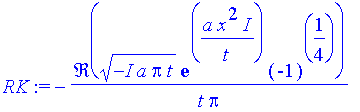
RK := -1/t/Pi*Re((-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)*(-1)^(1/4))

>    t:=Pi:a:=1:

>    pl1:=plot(RK,x=-10..10):pl1;

[Maple Plot]

>    #RK;

>   

>   

>    with(plots):

>    animate(RK,x=-5..5,t=0.2..2,numpoints=500,frames=15);

[Maple Plot]

>   

Leider ist der für kleine t und große x stark oszillierende Propagator keine Plot-freundliche Funktion. Man kann aber durch Einstellen der richtigen Perspektive den Überblick bekommen ...

>    plot3d(RK,x=0..10,t=.2..0.5,style=wireframe,grid=[50,50]);

[Maple Plot]

>   

Die Moire-Muster (3d) hängen von der Aulösung ab: im x-t-Diagramm sind die "Orte" gleicher Phase nichts anderes als die Parabeln t = x^2*const .

>   

>   

>    a:='a':t:='t':

>    assume(t>0,a>0);

>    IK:=evalc(Im(Kw));

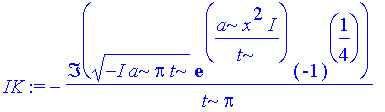
IK := -1/t/Pi*Im((-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)*(-1)^(1/4))

>    IK:=subs(t=th,a=ah,IK):

>    t:='t':a:='a':

>    IK:=subs(th=t,ah=a,IK);

IK := -1/t/Pi*Im((-I*a*Pi*t)^(1/2)*exp(a*x^2/t*I)*(-1)^(1/4))

>    t:=2:a:=1:

>    pl2:=spacecurve([IK,x,RK],x=-8..8,numpoints=500,axes=framed,color=black,orientation=[20,65]):pl2;

[Maple Plot]

>   

save pl1,pl2, `plpro.m`:


>    t:='t':

>    display([seq(spacecurve([IK,x,RK],x=-5..5,numpoints=400),t=seq(1+0.2*i,i=1..20))],insequence=true,

>    tickmarks=[0,0,0],axes=normal,orientation=[70,70]);

[Maple Plot]

>   

Wenn Feynman das gesehen hätte ... dann hätte er sicher auf Vollbild geschaltet, aber er war auch ohne Maple voll im Bild!

Aufgabe: Zeige, daß der Propagetor das Integral einer ebenen Wirkungswelle über alle Impulse ist. Wovon ist also der Propagator die Fouriertransformierte?

Aufgabe: Interpretiere die Fouriertransformierte in der Sprache der Pfadintegrale.

Aufgabe: Zeige, daß der Propagator der Grenzwert des Gauß-Schrödinger-Paketes ist für Ortsunschärfe -> 0.

(Aufgabe: relativistisch <-> NR)


>