Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 3.2.
Worksheet wellen1_10.mws
| > |
| > |
c International Thomson Publishing Bonn 1995 filename: wellen1
Autor: Komma Datum: Juli 94
Thema: Wellen, Wellengleichung
EINDIMENSIONAL
Standardzugang: "Welle = Schwingungen mit ortsabhängiger Phase, räumlich und zeitlich periodischer Vorgang, Energietransport ohne Massentransport. Also, wie schon in oszi.ms und mit der Wellenlänge lambda=2Pi/k:
| > | restart; with(plots):opt2d:=NULL:opt3d:=NULL: |
| > | y:=(x,t)->y0*cos(k*x-omega*t); |
![]()
Mit der zum Ort proportionalen Phase phi=k*x
| > | y0:=2: k:=2: omega:=3.5: |
| > | animate(y(x,t),x=0..6,t=0..1.9*Pi/omega,frames=20,numpoints=200); |
![[Maple Plot]](wellen1/wellen1_102.gif)
| > |
Sehen Sie eine horizontale oder eine vertikale Bewegung? Das hängt davon ab, wo und wie man hinschaut. Wenn man mit einem Blatt Papier das Bild bis auf die y-Achse abdeckt, sieht man eine vertikale Schwingung, wenn man horizontal bis fast zur Höhe y0 abdeckt, laufen Berge mit konstanter Geschwindigkeit. Aber das läßt sich natürlich auch "programmieren" (Sie können die beiden nächsten Animationen simultan laufen lassen):
| > | animate(y(x,t),x=0..0.05,t=0..1.9*Pi/omega,frames=20,numpoints=200,scaling=constrained,color=black); |
![[Maple Plot]](wellen1/wellen1_103.gif)
| > |
| > | animate(0.02*y(x,t),x=0..6,t=0..1.9*Pi/omega,frames=20,numpoints=200,scaling=constrained,color=red); |
![[Maple Plot]](wellen1/wellen1_104.gif)
| > |
Anstelle eines Blattes Papier kann man auch eine vertikale Blende nehmen. Durch ortsfeste Blenden sieht man die Schwingung eines Teilchens. Wie programmiert man eine ortsfeste Blende an der Stelle x0 mit der Breite delta?
| > | Blende:=(x0,delta)->(Heaviside(x-x0)-Heaviside(x-(x0+delta))); |
![]()
| > | #y0:='y0': k:='k': omega:='omega': |
| > | Teilchen1:=Blende(2, 0.08)*y(x,t); |
![]()
| > | Teilchen2:=Blende(3, 0.08)*y(x,t); |
![]()
| > | #y0:=2: k:=2: omega:=3.5: |
| > | animate({Teilchen1,Teilchen2,y(x,t)},x=0..6,t=0..1.9*Pi/omega,frames=20,numpoints=200,color=blue); |
![[Maple Plot]](wellen1/wellen1_108.gif)
| > |
Mit welcher Geschwindigkeit laufen die Berge? Das Argument der Winkelfunktion muß konstant sein: k*x-omega*t=const oder x=const/k+omega/k*t = x0 + c*t.
| > | Phase1:=Blende(omega/k*t, 0.08)*y(x,t); |
![]()
| > | animate({Teilchen1,Teilchen2,Phase1,y(x,t)},x=0..6,t=0..1.9*Pi/omega,frames=20,numpoints=200,color=blue); |
![[Maple Plot]](wellen1/wellen1_1010.gif)
| > |
Teilchen oder Welle? Das Teilchen schwingt, der Zustand (gr. Phase) bewegt sich gleichförmig. Das ist neu, daß sich etwas Immaterielles bewegt. Wie lautet die Bewegungsgleichung für diesen Vorgang? Die Bewegungsgleichung für einen Massenpunkt kennen wir, es ist die Schwingungsgleichung y''(t) =-omega^2*y(t) an einem Ort, d.h. die Ableitung ist partiell zu nehmen. Nur daß wir jetzt wegen der ortsabhängigen Phase unendlich viele solcher Schwingungsgleichungen haben, zwichen denen aber ein Zusammenhang besteht, wenn man x als Variable ansieht: y''(x)=-k^2*y(x) zu einer Zeit. Es ist also y''(t) ~ y(x,t) ~ y''(x) oder y''(t) ~ y''(x):
| > | y0:='y0': k:='k': omega:='omega': |
| > | wgl:=diff(y(x,t),t$2)=const*diff(y(x,t),x$2); |
![]()
| > |
| > | solve(%,const); |
![]()
Wir haben aber omega/k schon als Phasengeschwindigkeit c identifiziert, also gilt mit const=c^2 die partielle DG 2.Ordnung in den Variablen x und t:
| > | y:='y': |
| > | wgl:=diff(y(x,t),t$2)=c^2*diff(y(x,t),x$2); |
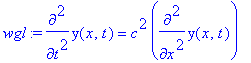
| > |
Nachdem wir nun "die Wellengleichung" aus einer Lösung konstruiert haben, können wir versuchen, Maple diese Gleichung lösen zu lassen. Denn die Konstruktion ist ja nicht zwingend -- es kann zu der gefundenen Gleichung noch andere Lösungen geben, genauso wie es zu "unserer Lösung" noch andere Bewegungsgleichungen geben kann.
| > |
| > | pdsolve(wgl,y(x,t)); |
![]()
Etwas ausführlicher:
Dazu müssen wir einen Weg finden, von der partiellen DG zur gewöhnlichen DG zu kommen, d.h. es darf nur eine unabhängige Variable auftauchen. Der Schlüssel dazu liegt in dem Ansatz, den wir schon oben gemacht haben. Wir zerlegen nach dem Motto y''(t) ~ y ~ y''(x) die Wellengleichung wieder in zwei Gleichungen yt''(t)=const und yx''(x)=const, wobei die Funktionen yt und yx jeweils nur von der einen Variablen t bzw. x abhängen. Die Funktion y(x,t) sollte also so gebaut sein, daß bei den partiellen Ableitungen nach der einen Variablen jeweils die unerwünschten Teile der Funktion verschwinden. Das geht sicher, wenn wir y(x,t) als Summe schreiben und folgenden Separationsansatz machen:
| > |
| > | y:='y':yt:='yt':yx:='yx': |
| > | y:=(x,t)->yt(t)+yx(x); |
![]()
Einsetzen in die Wellengleichung:
![]()
| > | wgl; |
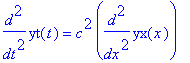
Kann Maple *diese* Gleichung lösen?
| > | dsolve(wgl,{yt(t),yx(x)}); |
Error, (in ODEtools/info) Required a specification of the indeterminate function
| > | pdsolve(wgl,yt(t)); |
Error, (in pdsolve/args) the indeterminate function, yt(t), depends on only one variable. Use solve or dsolve
| > |
Also müssen wir von Hand weiterrechnen:
| > | dglt:=lhs(wgl)=const; |
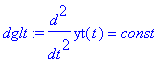
| > | dglx:=rhs(wgl)=const; |
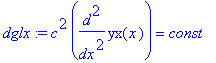
| > |
Auch im System akzeptiert Maple nicht mehr als eine unabhängige Variable, wir können jetzt aber die beiden gewöhnlichen Differentialgleichungen getrennt lösen.
| > | solt:=dsolve({dglt},{yt(t)}); |
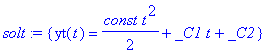
| > | solx:=dsolve({dglx},{yx(x)}); |
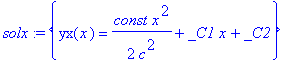
Das entspricht zwar nicht unseren Erwartungen (Schwingung), aber es ist eine Lösung der Wellengleichung!
| > | assign(solt,solx); 'y(x,t)'=y(x,t); wgl; |
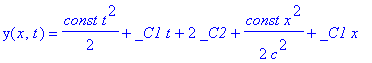
![]()
Aber wir können einen anderen Separationsansatz machen und y(x,t) als Produkt schreiben.
| > |
| > |
| > | t:='t':y:='y':y1:='y1': y2:='y2': const:='const': c:='c':wgl:=diff(y(x,t),t$2)=c^2*diff(y(x,t),x$2):_C1:='_C1': _C2:='_C2': |
| > | y:=(x,t)->y1(x)*y2(t); |
![]()
| > | wgl; |
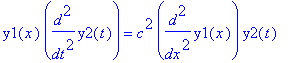
Noch etwas sortieren:
| > | wgl:=wgl/(y1(x)*y2(t)); |
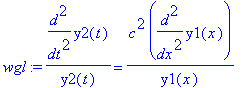
| > |
Diese Gleichung ist erfüllt, wenn beide Seiten ein und derselben Konstanten gleich sind (die explizite Lösung ist von Maple nur zu erhalten, wenn man die DGn vorher noch mit y1 bzw. y2 multipliziert)
| > | dglt:=(lhs(wgl)=const)*y2(t); |
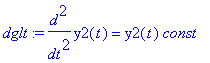
| > | #dglt:=(lhs(wgl)=const); |
| > |
| > | dglx:=(rhs(wgl)=const)*y1(x); |
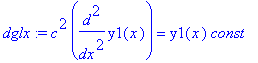
| > | solt:=dsolve({dglt},{y2(t)}); |
![]()
In Release 5 cosh, sinh statt exp.
Überflüssig in Maple > 6
| > | #convert(solt,exp); |
| > |
In früheren Releases wurden noch folgende Lösungen vorgeschlagen - nun auch wieder in Maple 10...:
| > | y2alt:=t->_C1*exp(sqrt(const)*t)+_C2*1/exp(sqrt(const)*t); |
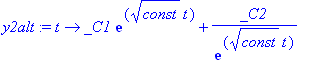
| > | y1alt:=x->_C1*exp(sqrt(const)*x)+_C2*1/exp(sqrt(const)*x); |
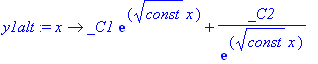
| > | solx:=dsolve({dglx},{y1(x)}); |
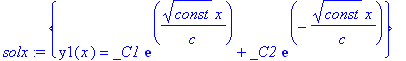
| > | assign(solt,solx); |
| > | y1:=unapply(y1(x),x);y2:=unapply(y2(t),t); |
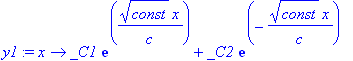
![]()
| > | simplify(wgl); |
![]()
| > |
Auch das sind also Lösungen der Wellengleichung. Wir wollen uns diese Lösungen anschauen. Damit sich die gewohnten Wellen ergeben, muß const<0 sein und wir stellen den Realteil einer Lösung über x und t dar. Wenn wir nur eine der beiden Integrationskonstanten von 0 verschieden wählen, bekommen wir eine "nach links" (zu kleineren x-Werten) laufende Welle und können die Momentanbilder in t-Richtung aufreihen.
| > |
Mit den 'alten Lösungen':
| > | y:=(x,t)->y1alt(x)*y2alt(t); |
![]()
| > |
| > | y(x,t); |
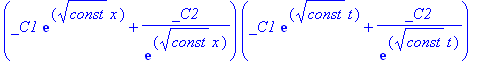
| > | _C1:=0: _C2:=1: const:=-20: c:=1/2: |
| > | plot3d(evalc(Re(y(x,t))),x=0..1,t=0..1,axes=boxed); |
![[Maple Plot]](wellen1/wellen1_1038.gif)
| > |
Aber natürlich ... auch laufen lassen und mit den _C's spielen
| > | _C1:=0:_C2:=1: |
| > |
| > | animate(evalc(Re(y(x,t))),x=0..1,t=0..2*Pi/sqrt(abs(const)),frames=20); |
![[Maple Plot]](wellen1/wellen1_1039.gif)
| > |
Auch der Parameter const, der für die Frequenz oder die Wellenlänge steht, kann verändert werden. Wenn man z.B. die Zeit festhält (y(x,'t') muß dann mit 't' aufgerufen werden), hat man eine Achse für den Parameter frei und kann -- einmal mehr -- den Übergang von der Periodizität zu aperiodischen Vorgängen zeigen. Und das sind alles Lösungen der "Wellengleichung".
| > | t:=0:const:='const': |
pspl(`p1well1.ps`):
| > | plot3d(evalc(Re(y(x,'t'))),x=0..1,const=-20..5); |
![[Maple Plot]](wellen1/wellen1_1040.gif)
| > |
Gerade hier lohnt sich wieder die Animation, und man sollte sich die Zeit und den Speicherplatz (ca. 3MB) nehmen und den Plot auf volle Bildgröße stellen aber auch den Stil der Darstellung ändern (z.B. contour), denn es gibt eine Menge zu sehen.
| > | t:='t':_C1:=0: _C2:=1: |
| > | animate3d(evalc(Re(y(x,'t'))),x=-1..1,const=-25..5,t=0..1,frames=15,axes=boxed,view=-1..3,style=hidden); |
![[Maple Plot]](wellen1/wellen1_1041.gif)
| > |
| > |
In (negative) x-Richtung laufen Wellen mit ein und derselben Geschwindigkeit (c), deren Wellenlänge für const -> 0 unendlich groß wird. Bei const=0 haben wir den "aperiodischen Grenzfall" mit der Frequenz 0 -- es ist keine Bewegung zu sehen. Für const>0 wird die Exponentialfunktion in x-Richtung verschoben. Eine unphysikalische Lösung der Wellengleichung? Nein, nur eine exponentiell abklingende Auslenkung zu einem bestimmten Startwert und mit verschiedenen "Zerfallskonstanten" ... man kann ja wieder den Blick auf ein Teilchen fixieren. Man kann aber auch die Parameterachse als Orientierung nehmen. Dort laufen Wellen mit abnehmender Wellenlänge in Richtung const=0 und darüber hinaus: Schwingungen verwandeln sich in abklingende Vorgänge. Wenn wir uns vorstellen, daß sich der Parameter längs einer realen räumlichen Dimension linear ändert, sehen wir den "Tunneleffekt" .. und die 4.Dimension sehen wir indirekt -- eben weil die Bilder laufen.
| > |
| > | #y:=(x,t)->y0*exp(I*(k*x-omega*t)); |
| > | #wgl; |
| > | #simplify("); |
| > | #solve(",c); |
| > | #simplify({"}); |
| > | #with(student): |
| > | #yx:=makeproc(rhs(solx),x); yt:=makeproc(rhs(solt),t); |
| > | #yw:=yx(x)*yt(t); |
| > | #yw:=combine(yw,power); |
| > | #evalc(yw); |
| > | #plot3d(Re(yw),x=0..1,t=0..1); |
| > |
Bei unserem ersten Versuch, die Wellengleichung durch eine Summe von Funktionen zu separieren, haben wir gesehen, daß auch ganz einfache Parabeln Lösung der Wellengleichung sind. Sie müssen sich nur mit der Geschwindigkeit c "bewegen". Läßt sich das verallgemeinern, ist also jede Funktion f(x,t), die eine Verschiebung darstellt, Lösung der Wellengleichung? Wenn ja, dann müßte
| > | #restart; |
| > | f:='f': y:='y': c:='c':t:='t': |
| > | y:=(x,t)->f(x-c*t); |
![]()
die Wellengleichung lösen, die wir mit der <inert-Version Diff aufstellen
| > | wgl:=Diff(y(x,t),t$2)=c^2*Diff(y(x,t),x$2); |
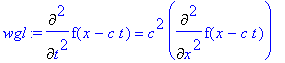
und dann mit <value auswerten, um nebenbei zu zeigen, wie weit man mit Maple das symbolische Rechnen treiben kann
| > | value(wgl); |
![]()
| > |
D^(2) bedeutet die äußere Ableitung (nach (x-c*t) in diesem Fall). Also ist jede Funktion von a*x+b*t Lösung der Wellengleichung (mit c^2=b^2/a^2). Nachdem über die Vorzeichen keine Voraussetzungen gemacht sind, bzw. c quadratisch vorkommt, bedeutet das auch, daß die Richtung der Verschiebung nicht festgelegt ist: x^2=c^2*t^2 ist eine bessere Charakterisierung des Vorganges als x=c*t. In der Theorie der partiellen Differentialgleichungen spricht man von den Charakteristiken der PDG (BS476,490). In diesem Fall sind das (ins Räumliche übertragen) die Flächen gleicher Phase oder Wellenfronten, auf die wir noch öfter zurückkommen werden. An dieser Stelle ist es aber wichtig festzuhalten, daß "alles was sich gleichförmig bewegt" als Lösung der Wellengleichung aufgefaßt werden kann -- um es einmal ein bißchen provokant zu formulieren -- z.B. auch ein starrer Körper, etwa ein Block der Länge a und der Höhe 1, den wir als Blende schon zur Verfügung haben:
| > | Blende:=(x0,delta)->(Heaviside(x-x0)-Heaviside(x-(x0+delta))); |
![]()
| > | Block:=Blende(c*t,a); |
![]()
| > | a:=2:c:=1/2: |
| > | animate(Block(x,t),x=-5..5,t=-4..4,frames=20);#,numpoints=200); |
![[Maple Plot]](wellen1/wellen1_1047.gif)
| > |
| > | a:='a': c:='c': |
| > | y:=(x,t)->Block; |
![]()
| > | wgl:=diff(y(x,t),t$2)=c^2*diff(y(x,t),x$2); |
![]()
| > |
Wenn auch nicht sofort verständlich sein mag, was da steht: die linke Seite ist gleich der rechten Seite und ... Maple kann mit diesen Funktionen umgehen (die Dirac-Funktion ist die Ableitung der Heaviside-Funktion und <Dirac(1,...) bedeutet die erste Ableitung). Aber versuchen Sie es selbst mit folgenden Beispielen -- und eigenen.
| > | c:='c': |
| > | y:='y':wgl:=diff(y(x,t),t$2)=c^2*diff(y(x,t),x$2): |
| > | f:='f': |
| > | y:=(x,t)->f(x-c*t);#+f(x+c*t); |
![]()
| > | f:=u->u^3-50*u; |
![]()
| > | #f:=sin; |
| > | #f:=tan: |
| > | #f:=ln: |
| > | #f:=w->(w-w^3)/(w^4+0.1); |
| > | f:=z->exp(-z^2); |
![]()
| > | wgl;simplify(lhs(wgl)-rhs(wgl)); |
![]()
![]()
| > |
Aber man kann mit Maple eben nicht "nur" mit beliebig vielen speziellen Beispielen testen, ob das, was man vorher mit Maple in allgemeiner Form bewiesen hat auch zutrifft, man kann sich auch ein bewegtes Bild davon machen.
| > | c:=1/2: |
| > | animate(y(x,t),x=-5..5,t=-5..10,frames=20,color=red); |
![[Maple Plot]](wellen1/wellen1_1055.gif)
| > |
Und wenn man mit diesen Bildern spielt, stellt man bald fest, daß die Wellengleichung eigentlich Verschiebungsgleichung heißen müßte. Es ist die allgemeinste Form einer Gleichung, die eine gleichförmige Bewegung beschreibt. Aber was bewegt sich nun wirklich?
Nach der Schuldefinition ist die Welle ein zeitlich und räumlich periodischer Vorgang, bei dem Energie aber keine Masse transportiert wird. Von der Periodizität haben wir schon Abschied genommen und Masse und Energie sind äquivalent, d.h. es bleibt nichts übrig von dieser Definition. Nur ein Zusatz, den man manchmal macht, bleibt übrig: "zwischen den einzelnen Punkten herrscht eine feste Phasenbeziehung". Aber das ist gerade die Beziehung der gleichförmigen Bewegung ... von ETWAS. Es ist nicht mehr der einzelne Massenpunkt der Newtonschen Mechanik, es muß nicht die Kontur eines starren Körpers sein, nicht eine Feldstärke oder eine Temperatur - es muß nicht schwingen: es muß nur ETWAS sein. Die Wellengleichung beschreibt die Bewegung von Information. Jetzt ist etwas da, jetzt ist es dort oder einfach nicht mehr da. Das Sein oder Nichtsein (Vorhandensein oder Nichtvorhandensein) wird aber auf eine indirekte Art beschrieben. (Viel da wenig da?) Sie können das dadurch testen, daß Sie zwei in entgegengesetzte Richtung laufende Informationen überlagern, also das assignment von y:=f(x-c*t) in y:=f(x-c*t)+f(x+c*t) ändern. Je nach Funktion läuft dann noch etwas oder es entsteht und verschwindet (manchmal natürlich auch periodisch). Sollten wir also die Wellengleichung nicht Informationsgleichung taufen?
Bevor wir aber den Fragen zu "der Wellengleichung" noch weiter nachgehen, wollen wir die Fragestellung an sich noch erweitern: gibt es nur diese eine Wellengleichung?
Als Forderung wieder die Verschiebung, also
| > | f:='f': |
| > | y:=(x,t)->f(k*x-omega*t);#+f(k*x+omega*t); |
![]()
Bei der Schwingungsgleichung kommt man im Prinzip mit einer DG 1.Ordng. aus. Reicht also eine PDG 1.Ordnung?
| > | testgl:=diff(y(x,t),t) = const*diff(y(x,t),x); |
![]()
| > | solve(testgl,const); |
![]()
| > |
Das wäre (für passendes omega und k) die gleiche Konstante wie oben, allerdings spielt nun das Vorzeichen von k eine Rolle, bzw. für f(+-) müßte die Differenz der Ableitung gleich der Summe der Ableitung sein. Das sind Einschränkungen auf nicht isotrope Vorgänge.
Reicht die erste Ableitung in einer Variablen, z.B. t?
| > | y:='y':f:='f': |
| > | sgl:=diff(y(x,t),t) = const*diff(diff(y(x,t),x),x); |
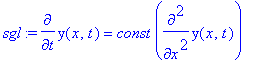
| > | y:=(x,t)->f(k*x-omega*t);#+f(k*x+omega*t); |
![]()
| > | sgl; |
![]()
| > | solve(sgl,const); |
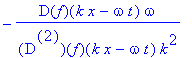
| > |
Das bedeutet eine Einschränkung auf Funktionen mit f'' ~ f', also Exponentialfunktionen, aus denen sich aber einiges zusammensetzen läßt [siehe Fourier]. Diesmal müßte omega/k^2=const sein, was sicher möglich ist -- verglichen mit omega/k=const. Und es kommt auf das Vorzeichen von k nicht an, die Isotropie ist gewährleistet. Aber es wird eine Richtung der Zeit ausgezeichnet (bzw. die sgl muß je Zeitrichtung anders geschrieben werden ... sgl ist NR -> psi+-).
Treiben wir ein bißchen experimentelle Mathematik, es kostet ja nichts:
| > |
| > | f:=u->u^3; |
![]()
| > | #f:=exp: |
| > | #f:=cos: |
| > | solve(sgl,const); |
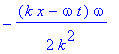
| > |
Polynome kommen als Lösung dieser "reduzierten DG" nicht in Frage, einfache trigonometrische Funktionen auch nicht. Exponentialfunktionen schon. Aber da gibt es doch eine Verbindung exp-sincos:
| > | f:=u->exp(I*u): sgl; |
![]()
| > | solve(sgl,const); |
![]()
| > | #simplify(%); |
Wenn wir also die Schwingung -- und damit die Superposition von Schwingungen -- ins Spiel bringen wollen, geht das bei dieser sgl nur, wenn wir es komplex formulieren. Diese Gleichung beschreibt aber in jedem Fall Diffusionsvorgänge, aperiodische, inkohärente, wenn man im Reellen bleibt.
WICHTIG: exp-Fkt.: 1.) Diffusion 2.) Schwingung!
| > | #y:=(x,t)->f(k*x-omega*t);#+f(k*x+omega*t); |
Die andere Variante (2.Ableitung nach der Zeit, 1.Ableitung nach dem Ort):
| > | f:='f': |
| > | xgl:=diff(y(x,t),t$2) = const*diff(y(x,t),x); |
![]()
| > | solve(xgl,const); |
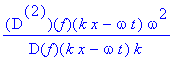
| > | f:=u->exp(I*u):xgl; |
![]()
| > | solve(xgl,const); |
![]()
| > | #simplify(%); |
| > |
Liefert wieder Anisotropie und als Proportionalitätskonstante eine Beschleunigung bzw. Kraft (im Gegensatz zur Schrödingergleichung, wo die Konstante eine Wirkung ist, bzw. Wirkung /Masse). Das wären also "Kraftwellen" ...
| > |
komma@oe.uni-tuebingen.de