PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 4.1.1

Worksheet wirf1a_10.mws

c International Thomson Publishing Bonn   1995                          filename: wirf1a.ms

Autor: Komma                                                                             Datum: 28.3.94

Thema: Wirkungsfunktion, Beispiele zur Veranschaulichung von T,V,L,S:

            a) gleichförmige und  gleichmäßig beschleunigte Bewegung, Schwingung (analytisch).

            b) Stückweise gleichf. Bewegung als Prototyp der linearen Approximation:

                3d-Darst. und Kurven gleicher Wirkung

Wir untersuchen zunächst die Wirkungsfunktion als solche an den Standardbeispielen der gleichmäßig beschleunigten Bewegung und der harmonischen Schwingung. Dazu müssen wir die kinetische Energie T, die potentielle Energie V, die Lagrangefunkion L und die Wirkungsfunktion S definieren:

>	restart; with(plots):

>	T:=m/2*v^2; v:=diff(x(t),t); L:=T-V; S:=int(L,t=t0..t1); H:=T+V;

>

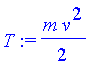
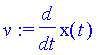
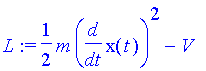
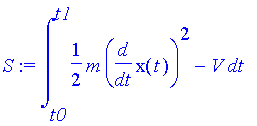
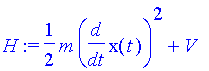
Es ist dabei zweckmäßig, die Geschwindigkeit v erst nach T zu definieren (späte Bindung). Die gesamte Energie H kann man zur Kontrolle verwenden.

Die Weg-Zeit Funktionen und die potentiellen Energien der beiden Bewegungstypen können wir als table-Einträge zur Verfügung stellen:

>	#x:=t->v0*t; #die gleichförmige Bewegung nur zu Testzwecken

>	xp[glb]:=t->-1/2*g*t^2+v0*t; #gleichmäßig beschleunigte Bewegung

>	xp[osz]:=t->sin(omega*t); #Schwingung

>	Vp[glb]:=m*g*xp[glb](t); #glm. beschl. Bew.

>	Vp[osz]:=1/2*k*xp[osz](t)^2; omega:=sqrt(k/m);

>

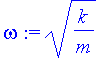
Mit der Miniprozedur typ() können wir auf den gewünschten Bewegungstyp umschalten. Wer andere Bewegungen untersuchen will, kann die entsprechenden Einträge hinzufügen und so das Computer-Algebra-System für sich arbeiten lassen.

>	typ:=proc(var) global x,V;

>	x:=xp[var]; V:=Vp[var];

>

end;

>

Wir wählen vereinfachend t0=0 und können uns nun die gesuchten Funktionen anzeigen lassen

>	t1:='t1': t0:=0:

>	#v0:='v0':

>	#typ(osz); T; S;

>	typ(glb); T; S;

>

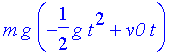
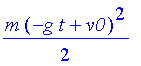
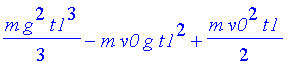
(Anhand der Typ-Einträge lassen sich die weitverzweigten Möglichkeiten eines CAS erahnen: man kann sich seine eigene Formelsammlung schreiben ...)

Nun können für die graphische Darstellung Zahlen eingesetzt werden. Die Variable St wird zur einheitlichen Darstellung bzw. zur Vereinfachung des Plotbefehls eingeführt.

>	typ(glb); #Reihenfolge!

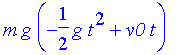
>	g:=10:  v0:=5: k:=2: m:=1:

>	#typ(osz): # Reihenfolge !

>	St:=subs(t1=t,S):

>	'T'  =T;'V' =V;'L'=L;'S'=St;'H'=H;

>

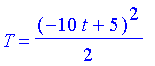
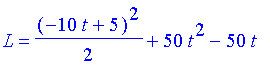
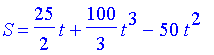
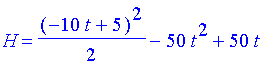
>	plot({T,St,L,V,H},t=0..2);

>

Bitte beim loopen auf die Reihenfolge der Zuweisungen von typ und Parametern achten (im Zweifelsfall zurück zu restart).

In dieser Art läßt sich also die Wirkung untersuchen und darstellen, wenn die Bewegung bekannt ist. Das eigentliche Ziel ist aber genau die Umkehrung. Wie erhält man aus der Wirkung, genauer gesagt aus dem Wirkungsprinzip, die Bewegung?

Das Wirkungsprinzip ist ein Variationsprinzip, das die wirkliche Bahn aus allen möglichen aussondert. Deshalb wollen wir zunächst am einfachsten Fall, nämlich der (eindimensionalen) gleichförmigen Bewegung, untersuchen, wie die Wirkung von "falschen" oder "nur gedachten" Bewegungen aussieht. Diese Überlegungen mögen auf den ersten Blick trivial erscheinen. Sie liefern aber eine weit tragende Methode, die wir sogar noch bei den Pfadintegralen verwenden können, nämlich die Bestimmung der Wirkungsfunktion durch lineare Approximation.

Wir gehen aus von einer kräftefreien Bewegung von x = 0 nach x = x1, die in der Zeit t1 ablaufen soll, und ersezten sie durch eine stückweise gleichförmige Bewegung mit gleichem Anfangs- und Endpunkt (im x-t-Diagramm), aber mit einem Zwischenpunkt P(t|x).

>	restart; with(plots):

>	pl1:=plot([[0,0],[5,6]],scaling=constrained,color=red):pl2:=plot([[0,0],[2,5],[5,6]],scaling=constrained):

>	pkte:=plot([[0,0],[2,5],[5,6]],style=point,symbol=circle,scaling=constrained):

>	tp:=textplot([[2.5,4.5,`P(t|x)`],[6,5.5,`P1(t1|x1)`]]): display({pl1,pl2,pkte,tp});

>

>

Für diese variierte Bahn kann man als Maß für die Wirkung einfach die Summe der kinetischen Energien auf den beiden Teilstücken nehmen. Diese Summe muß immer größer sein als die kinetische Energie der Bewegung ohne Geschwindigkeitsänderung. Nachdem es nur um Extremalwerte geht, können wir auch noch Proportionalitätsfaktoren wie m/2 vernachlässigen und mit folgendem S rechnen:

>	S:=x^2/t+(x1-x)^2/(t1-t);

>

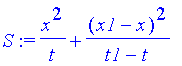
Ordnet man jedem Zwischenpunkt P im x-t-Diagramm diese Wirkung als Ordinate zu, so muß ein Tal sichtbar werden, dessen tiefste Punkte über der wirklichen Bahn liegen:

>	t1:=2: x1:=3:

>	plot3d(S,t=0.1..1.9,x=x1/t1*t-1..x1/t1*t+1,view=0..10,axes=boxed);

>

Zwei weitere Darstellungsmöglichkeiten:

>	#contourplot(S,t=0.1..1.9,x=x1/t1*t-1..x1/t1*t+1,axes=boxed,contours=20);

>	contourplot(S,t=0.1..1.9,x=-1..3,axes=boxed,contours=20);

>

>

>

>	gradplot(-S,t=.3..1.8,x=0.2..2.8,axes=boxed,arrows=THICK);

>

Durch die Grenzen in den Plot-Befehlen wurden die Pole der Funktion S(t) ausgespart und damit auch die Zeiten jenseits der Pole.

Was geschieht, wenn wir auch Zwischenpunkte zulassen, die eine Bewegung erfordern, die zeitlich rückwärts läuft (t > t1 oder t < 0)? Natürlich treten dann zunächst bei t = 0, t1 Pole auf, da in diesen Fällen die Geschwindigkeit unendlich groß wird. Aber jenseits der Pole ist die Wirkung immer noch definiert und sie bekommt in der QED sogar dort noch einen Sinn.

>	plot3d(S,t=-1..3,x=-1..2,view=-20..20,axes=boxed);

>	#contourplot(S,t=-1..3,x=-1..2,axes=boxed);

[Bei den Plots auch darauf achten, daß Vorwärts- und Rückwärtsbewegung erlaubt ist. Günstige Arten der Darstellung suchen wie z.B. Höhenlinien, Logarithmus ...]

Doch zunächst regen die erzeugten Plots dazu an, die Kurven gleicher Wirkung (Höhenlinien) näher zu untersuchen. Man kann dies am einfachsten mit dem Befehl <implicitplot:

>	implicitplot(S=5,t=-1..1.9,x=-1..4);

>

Bei den  Polen scheint Maple Schwierigkeiten zu bekommen. Wir können unserem CAS aber ein bißchen helfen, indem wir die Gleichung für die konstante Wirkung C etwas umformen.

>	x1:='x1':t1:='t1':

>	gl:=S*t*(t1-t)=C*t*(t1-t);

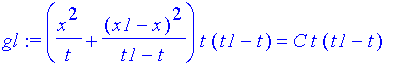
>	gl:=simplify(gl);

(Die Berechnung der nächsten Plotstruktur dauert etwas länger.)

>	C:='C':x1:=2:t1:=2:

>	implicitplot({seq(gl,C=-10..10)},t=-1..4,x=-1..3);

>

So sehen also die Kurven gleicher Wirkung bei der stückweise gleichförmigen Bewegung aus: Ellipsen für Bewegungen, die in der Zeit vorwärts laufen, Hyperbeln für Bewegungen, die in der Zeit rückwärts laufen.

Man würde gerne weiter untersuchen, ob die Zeitrichtung etwas mit der Geometrie zu tun hat (Euklid oder Minkowski).

>

>

komma@oe.uni-tuebingen.de