Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 4.1
Worksheet wirf3_10.mws
c International Thomson Publishing Bonn 1995 filename: wirf3.ms
Autor: Komma Datum: 28.3.94
Thema: Wirkungsfunktion des harmonischen Oszillators:
Näherungslösung durch schwaches Extremum der Wirkungsfunktion,
wenn die Ortsfunktion als Polynom n-ten Grades angesetzt wird.
Vergleich mit der Reihenentwicklung der exakten Lösung.
Die Bewegung des harmonischen Oszillators kann ebenfalls über das schwache Minimum der Wirkungsfunktion näherungsweise bestimmt werden, wenn wir zum Beispiel ein Polynom n-ten Grades ansetzen.
| > | restart; |
| > | T:=m/2*v^2: v:=diff(x(t),t): L:=T-V: S:=int(L,t=t0..t1): t0:=0: |
| > |
Das Polynom n-ten Grades durch die zwei Punkte (0|0) und (t1|x1) bauen wir zur Abwechslung mit Hilfe des Punkt-Operators (cat) auf:
| > | n:=10; |
![]()
| > | xx:=proc(t) local xx,i; |
| > | xx:=0; |
| > | for i to n do |
| > | xx:=xx+a||i*t^i; |
| > | od; |
| > |
| > | RETURN(xx); |
| > | end; |
![]()
| > |
Ein Koeffizient (z.B. a1) läßt sich durch die Bedingung x(t1)=x1 und die anderen Koeff. ausdrücken:
| > | as1:=solve(xx(t1)=x1,a1); |
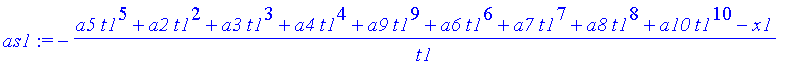
| > |
Unser CAS liefert uns auf Knopfdruck die Weg-Zeit-Funktion zu den aufgestellten Bedingungen.
| > | x:=t->subs(a1=as1,xx(t)): |
| > | x(t); |
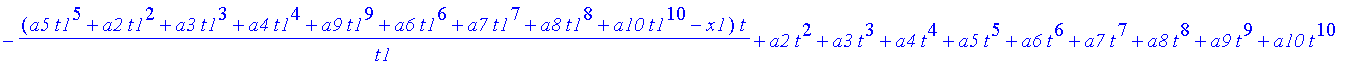
| > |
Und mit dem qudratischen Potential
| > | k:='k': |
| > | V:=1/2*k*x(t)^2: |
erhalten wir für die Wirkung einen etwas längeren Ausdruck ...
| > | Ss:=simplify(S); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wir stellen wieder unser Gleichungssystem auf und lassen es lösen.
| > |
| > | #x(t); |
| > |
| > | sys:=seq(diff(Ss,a||j),j=2..n): |
| > | #sys; |
| > |
| > | #a.(2..n); |
| > | # Probleme in R4!erst Werte einsetzen! |
| > | # R5 packt es wieder, aber langsamer als R3 |
| > | # schnelle Lösung in R6 |
| > | sol:=solve({sys},{a||(2..n)}): |
| > |
| > | #sol; |
| > |
| > |
Wenn Sie sich die Lösung xs im Worksheet ausgeben lassen, werden Sie sicher meine Begeisterung für dieses CAS teilen: Probleme, die von der Struktur her einfach sind, jedoch einen immensen Rechenaufwand bedeuten würden, wollte man sie von Hand lösen, sind ein gefundenes Fressen für Maple. Hier kann man zuschauen, wie Quantität in Qualität umschlägt, und - was ebenso wichtig ist - man kann damit weiterarbeiten.
| > | xs:=subs(sol,x(t)): |
Nun können wir Zahlen für die Federkonstante, die Masse und den Endpunkt einsetzen
| > | k:=2: m:=1/4: t1:=2: x1:=3: |
und für eine vergleichende Darstellung die exakte Lösung der Newton-DGL parat stellen.
| > | exakt:=rhs(dsolve({diff(y(t),t$2)=-k/m*y(t),y(0)=0,y(t1)=3},y(t))); |
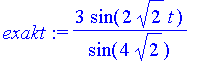
| > | simplify(exakt,trig); |
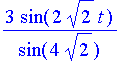
| > |
| > | #plot({exakt},t=-1..t1+1,-10..10); |
| > | plot({exakt,xs},t=-1..t1+1,-10..10); |
![[Maple Plot]](wirf3/wirf3_1024.gif)
| > |
Der Vergleich unseres Näherungspolynoms mit der exakten Lösung ist aber nicht "nur" graphisch möglich. Man kann mit Hilfe der Reihenentwicklung der exakten Lösung auch untersuchen, welche Koeffizienten eine Abweichung verursachen bzw. was eine Erhöhung der Ordnung bewirkt.
| > | evalf(series(exakt,t,10)); |
![]()
| > | evalf(xs); |
![]()
![]()
| > |
komma@oe.uni-tuebingen.de