
Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 5.2.2
Worksheet wiwe2_10.mws
c International Thomson Publishing Bonn 1995 filename: wiwe2
Autor: Komma Datum: 9.9.94
Thema: Wirkungswellen im Coulombfeld
************* Stammdatei zur weiteren Bearbeitung in R5. Insbesondere wegen Fehler bei der Fallunterscheidung in R5 (komplexe Zahlen). Aus R3/4 wurden die Ausdrücke wc4 und wppm4 kopiert. Damit läuft es.
Input-fonts ggf. auf Courier stellen, wegen I, l, und 1. Aus dem gleichen Grund wurde für den Drehimpuls der Buchstabe L gewählt. (Student Edition: array size < 5120)
Wirkungswellen im Coulombfeld
Im 1/r-Potential (pot. Energie V=-k/r) beschreibt ein Körper der Masse m, mit der Gesamtenergie H und dem Drehimpuls L die Bahn
| > | restart:with(plots): |
| > | bahnr:=p/(1+epsilon*cos(phi-alpha)); |

Dabei gilt für die Exzentrizität epsilon
| > | epsilon:=sqrt(1+2*H*L^2/m/k^2); |

und für den Halbparameter p
| > | p:=L^2/m/k; |

Der maximale Drehimpuls ist bei negativer Gesamtenergie:
| > | Lm:=sqrt(-m*k^2/2/H); |
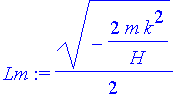
Bekanntlich beschreibt die Bahngleichung in Polarkoordinaten für epsilon>1 (H>0) Hyperbeln, für epsilon=1 (H=0) Parabeln und für 0<epsilon<1 (H<0, L<=Lm) Ellipsen. Wir können die aufgestellten Beziehungen testen, indem wir zunächst die Darstellung konfokaler Ellipsen zu gegebenem H und einer Reihe von Drehimpulsen erzeugen:
| > | m:=1: k:=1: |
| > | H:=-0.1: alpha:=0: |
| > | epsilon;Lm; |
![]()
![]()
| > | polarplot({seq([bahnr,phi,phi=0..2*Pi], |
| > | L=seq(i*(Lm-10^(-3))/5+10^(-3),i=0..5))},scaling=constrained,color=red,axes=boxed); |
![[Maple Plot]](wiwe2/wiwe2_107.gif)
| > |
Interessanter ist aber die Frage, welche Wirkungswellen zur Bewegung im Coulomb-Potential gehören.
Das System wird durch H und L beschrieben, es bleibt also alpha frei und damit entsteht eine Schar von Ellipsen, die um den gemeinsamen Brennpunkt gedreht sind, z.B.
| > | alpha:='alpha':L:=2: |
| > | elli:=polarplot({seq([bahnr,phi,phi=0..2*Pi], |
| > | alpha=seq(i*Pi/4,i=0..7))},scaling=constrained,color=red): |
| > | elli; |
![[Maple Plot]](wiwe2/wiwe2_108.gif)
| > |
Das Ergebnis speichern wir für später unter dem Namen elli ab. Der Darstellung entnimmt man, daß die Bewegung innerhalb zweier Kreise (den Apsidenkreisen) stattfindet. Sie haben die Radien
| > | H:='H':L:='L': |
| > | rad:=2*(H*r^2+r)-L^2: |
| > | r12:=solve(rad,r): |
| > | r1:=r12[1]; r2:=r12[2];#H<0 |


| > |
Für H>0 ist die Bewegung nicht gebunden. Es wäre aber nicht zweckmäßig, wegen dieser Fallunterscheidung ein neues Worksheet zu schreiben, also fahren wir im Folgenden zweigleisig:
Hyperbel: H>0
Zur Erzeugung einer Hyperbelschar kann man den zweiten Ast durch geeignete Wahl des Winkelbereiches unterdrücken (Delta meidet die Asymptoten, Alternative: option discont=true)
| > | alpha:='alpha': H:='H': L:='L': |
| > | ph1:=alpha-arccos(-1/epsilon); ph2:=alpha+arccos(-1/epsilon); |


| > | H:=0.2: L:=2: m:=1: k:=1:delta:=1/10: |
| > | polarplot({seq([bahnr,phi,phi=ph1+delta..ph2-delta], |
| > | alpha=seq(i*Pi/4,i=0..7))},scaling=constrained,color=black,view=[-15..15,-15..15]); |
![[Maple Plot]](wiwe2/wiwe2_1013.gif)
| > |
Wir speichern zur späteren Verwendung von dem einen Hyperbelast nur die Hälfte ab:
| > | hyp:=polarplot({seq([bahnr,phi,phi=alpha..ph2-delta], |
| > | alpha=seq(i*Pi/4,i=0..7))},scaling=constrained,color=black,view=[-15..15,-15..15]): |
| > | hyp; |
![[Maple Plot]](wiwe2/wiwe2_1014.gif)
| > |
Den Sonderfall der Parabel können wir später behandeln. Wir folgen dem Gedankengang "mögliche Bahnen sind die Orthoganaltrajektorien zu den Wellenfronten der Wirkungswellen" und suchen also diese Wellenfronten.
Die charakteristische Funktion W läßt sich im Zentralfeld in einen radialen Anteil wr und einen azimuthalen Anteil wp zerlegen.
| > |
| > | wr:='wr': wp:='wp': |
| > | w:=wr+wp; |
![]()
Der azimuthale Anteil ist problemlos
| > | L:='L': |
| > | wp:=L*phi; |
![]()
Der radiale Anteil lautet
| > | H:='H': m:='m': k:='k': |
| > | wr:=int(sqrt(2*m*(H+k/r)-L^2/r^2),r); |
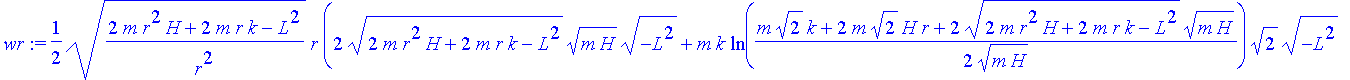

| > |
Und wird von MapleR3 nicht integriert.
Wir können aber etwas nachhelfen, wenn wir den Integranden umformen (die Konstanten m und k werden mitgeführt, falls Sie später mit konkreten Zahlen arbeiten wollen)
| > | rad:=2*m*(H*r^2+k*r)-L^2; |
![]()
| > | wr:=int(sqrt(rad)/r,r); |

Wir informieren uns über das Verhalten von wr am Beispiel der Ellipsenbahnen
| > | H:=-0.1: L:=2: m:=1: k:=1: |
| > | plot({evalc(Re(wr)),evalc(Im(wr))},r=r1-2..r2+2); |
![[Maple Plot]](wiwe2/wiwe2_1021.gif)
| > |
| > |
| > | #r1;r2; |
| > |
Zwischen den Apsidenkreisen ist wr reell !! nicht mehr in Maple 6 !!! (Re(wr) muß für den Plot dennoch angegeben werden).
Für die Darstellung der Iso-W-Linien (Linien gleicher Wirkung) können wir die Gleichung w=const nach phi auflösen
| > | L:='L': H:='H': |
| > | const:='const': |
| > | #assume(L>0,H<0); |
| > | wc:=solve(w=const,phi); |
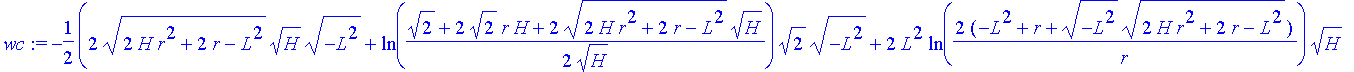

| > | simplify(wc); |

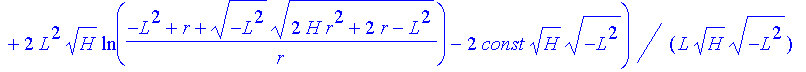
| > | #w; |
| > |
| > | # Einfache Lösung aus Release 4 NICHT LÖSCHEN !! |
| > | wc4 := -((2*H*r^2+2*r-L^2)^(1/2)+1/2*2^(1/2)/H^(1/2)*ln(2^(1/2)*H^(1/2)*(r+1/2/H)+(2*H*r^2+2*r-L^2)^(1/2))+L^2/(-L^2)^(1/2)*arctanh(1/2*(-2*L^2+2*r)/(-L^2)^(1/2)/(2*H*r^2+2*r-L^2)^(1/2))-const)/L; |

| > |
| > |
| > |
und für die oben getroffene Wahl der Parameter darstellen
| > | H:=-0.1: L:=2:r2; |
![]()
| > | wc;#wc4; |

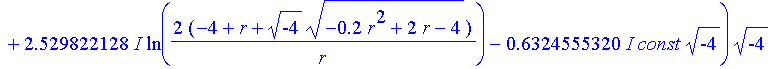
| > |
| > | const:=1: |
| > | plot([evalc(Re(wc)),evalc(Re(wc4))],r=0..r2+1,color=[red,blue]); |
![[Maple Plot]](wiwe2/wiwe2_1030.gif)
| > | # Seltsame Ergebnisse in Maple 6!!!!!!!!!!!!!! |
| > | # Weiterhin Probleme mit Fallunterscheidung in R6 |
| > |
| > | #evalc(Re(wc)); |
| > | const:='const':with(plots): |
| > | welli:=polarplot({seq([r,evalc(Re(wc4)),r=0..r2+1], |
| > | const=seq(i*L*Pi/4,i=0..7))},scaling=constrained,color=black): |
| > | welli; |
![[Maple Plot]](wiwe2/wiwe2_1031.gif)
Nun sollten die orthogonalen Kurvenscharen zu sehen sein, nämlich Wellenfronten, die senkrecht auf allen Ellipsenbahnen mit gleichem L und H stehen.
| > | display({elli,welli}); |
![[Maple Plot]](wiwe2/wiwe2_1032.gif)
| > | # falls sich jemand für den Imaginaerteil interessiert ... |
| > | #iwelli:=polarplot({seq([r,evalc(Im(wpp)),r=0..r2+1], |
| > | #const=seq(I*i*L*Pi/4,i=0..1))},scaling=constrained,color=black): |
Es scheint zu funktionieren. Auch bei Hyperbeln? Ja, wenn man etwas länger wartet.
| > | H:=0.2:# hier läuft es mit wc: H>0 |
| > | r1;L; |
![]()
![]()
| > | # hier braucht man den Realteil von wc |
| > | whyp:=polarplot({seq([r,Re(wc),r=r1..15], |
| > | const=seq(i*L*Pi/4,i=0..7))},scaling=constrained,color=red,view=[-15..15,-15..15]): |
| > | whyp; |
![[Maple Plot]](wiwe2/wiwe2_1035.gif)
| > |
| > | #wc; |
| > | # zur Interferenz (s.u.) |
| > | #whypm:=polarplot({seq([r,wppm,r=r1..15], |
| > | #const=seq(i*L*Pi/4,i=0..1))},scaling=constrained,color=red,view=[-15..15,-15..15]): |
| > | display({hyp,whyp}); |
![[Maple Plot]](wiwe2/wiwe2_1036.gif)
| > |
****************************
Zur Untersuchung des Parabelsonderfalls (H=0) können die folgenden Zeilen mit F5 zu Input umgewandelt werden. Interessant: H=0 bedeutet "statische Wellen".
H:=0:L:='L':
w0:=int(sqrt(2*(H*r^2+r)-L^2)/r,r);
H:='H':
wp0:=w0+L*phi;
const:='const': L:='L':
wpp0:=solve(wp0=const,phi);
L:=2:H:=0:
par:=polarplot({seq([p/(1+eps*cos(phi-alpha)),phi,phi=ph1..ph2-delta],
alpha=seq(i*Pi/4,i=0..7))},scaling=constrained,color=black,view=[-15..15,-15..15]):
par;
wpar:=polarplot({seq([r,wpp0,r=0..15],
const=seq(i*L*Pi/4,i=0..7))},scaling=constrained,color=red,view=[-15..15,-15..15]):
wpar;
display({par,wpar});
**************************
Wir haben also die orthogonalen Kurvenscharen gefunden -- diesmal direkt mit Hilfe der Wirkungsfunktion, also ohne DG -- und können zur Darstellung der Wellen übergehen. Im ersten Schritt interessiert nur die räumliche Verteilung, die zur charakteristischen Funktion W gehört:
| > | H:='H':L:='L': |
| > | psi:=exp(I*w); |

| > | #psim:=exp(I*(-w+L*phi)); |
| > | #psi0:=exp(I*(w0+L*phi)); |
Für die plots stellen wir den Realteil und den Imaginärteil der Wellen parat:
| > | rpsi:=evalc(Re(psi)): |
| > | ipsi:=evalc(Im(psi)): |
Parabel
rpsi0:=evalc(Re(psi0)):
ipsi0:=evalc(Im(psi0)):
Keine Animation wegen H=0
Und so sehen die Wellen zu Hyperbelbahnen aus (für H>0 wird r2<0, deswegen ist in den nächsten Plots eine Konstante für die obere Grenze des Radius eingestzt. Sie können aber auch mit abs(r2) arbeiten):
| > | H:=0.2:L:=1:phi:='phi': |
| > | plot3d([r*cos(phi),r*sin(phi),rpsi],r=r1..30,phi=0..2*Pi,style=hidden,axes=boxed,orientation=[45,17]); |
![[Maple Plot]](wiwe2/wiwe2_1038.gif)
Und wir haben als Kontrolle die Möglichkeit des Contourplots von Iso-W-Linien
| > | wwhyp:=contourplot([r*cos(phi),r*sin(phi),rpsi],r=r1..15,phi=0..2*Pi,scaling=constrained,axes=boxed, |
| > | numpoints=1000): |
| > | wwhyp; |
![[Maple Plot]](wiwe2/wiwe2_1039.gif)
Dieser Contourplot läßt sich aber nicht (mit display) zusammen mit dem 2d-Plot darstellen.
| > | display({wwhyp,hyp}); |
![[Maple Plot]](wiwe2/wiwe2_1040.gif)
Ein Vergleich in zwei getrennten plots ist aber immer möglich (falls whyp noch existiert)
| > | whyp; |
![[Maple Plot]](wiwe2/wiwe2_1041.gif)
| > |
| > |
Nun können Sie experimentieren und sich folgende Fragen beantworten:
Wie ändern sich die Wirkungswellen mit dem Bewegungstyp (H<0, H>0)?
Was bewirkt eine Änderung des Drehimpulses?
Gibt es Drehimpulse, die zu "besonderen Wirkungswellen" führen?
Wie sehen die Wirkungswellen außerhalb der Apsidenkreise aus?
Wie sieht der Imaginärteil aus?
Wie sieht die Radialbewegung aus? (Grenzwert von w für L -> 0)
Hier noch eine Anregung zum Darstellungsstil (den Sie auch im Plot ändern können):
| > | H:=-0.1: L:=3/2: # mit diesem L=3/2 scheint etwas nicht aufzugehen ... |
| > | plot3d([r*cos(phi),r*sin(phi),rpsi],r=r1..r2+5,phi=0..2*Pi,style=patchcontour,axes=boxed, |
| > | orientation=[45,10],grid=[50,50]); |
![[Maple Plot]](wiwe2/wiwe2_1042.gif)
| > |
| > | H:='H': L:='L': |
| > | psit:=psi*exp(-I*H*t); |

| > | rpsit:=evalc(Re(psit)): |
| > | n:=20: H:=-0.1: L:=2: |
| > | animate3d([r*cos(phi),r*sin(phi),rpsit],r=r1..r2+5,phi=0..2*Pi,t=0..2*Pi/abs(H)*(1-1/n), |
| > | style=wireframe,axes=boxed,frames=n,orientation=[30,7]); |
![[Maple Plot]](wiwe2/wiwe2_1044.gif)
| > |
... Wenn Schrödinger das gesehen hätte ... aber er hat es ja gesehen, auch ohne Maple ... eben virtuell.
Iso-W-Linien für Parabelbahnen keine Animation wegen H=0
L:=2:
contourplot([r*cos(phi),r*sin(phi),rpsi0],r=0.2..10,phi=0..2*Pi,axes=boxed,numpoints=2000,scaling=constrained);
| > |
Interferenz
Aber -- wie schon beim Wurf : die Wirkungswellen wären keine echten Wellen, wenn sie nicht interferieren könnten. Unabhängig vom Bahn- oder Wellentyp schneiden sich in jedem Punkt (außerhalb des inneren Apsidenkreises) genau zwei Bahnen bzw. Wellenfronten, die zu einer aufsteigenden und einer absteigenden Bewegung gehören. Es müssen also die zugehörigen Wellen überlagert werden. Allerdings ist bei der Superposition von "aufsteigend" und "absteigend" darauf zu achten, daß es sich um Bewegungen mit einem festen Drehsinn handelt, der durch L*phi-H*t festgelegt ist. Wir müssen also die Funktion wpm=-wr+L*phi bilden und nicht wpm=wr-L*phi, denn für die letztere hätte man Interferenz von gegenläufigen Bahnen und damit radiale Unabhängigkeit, während das Amplitudenquadrat aber azimuthal abhängig wäre . Zunächst der Plot der Iso-W-Linien
| > | H:='H':L:='L': |
| > | #wp:=wr+L*phi; |
| > | wpm:=-wr+L*phi; |

| > | const:='const': |
| > | wppm:=solve(wpm=const,phi); |


| > | # wieder mit Ergebnissen aus R4 |
| > | wppm4:= -(-(2*H*r^2+2*r-L^2)^(1/2)-1/2*2^(1/2)/H^(1/2)*ln(2^(1/2)*H^(1/2)*(r+1/2/H)+(2*H*r^2+2*r-L^2)^(1/2))-L^2/(-L^2)^(1/2)*arctanh(1/2*(-2*L^2+2*r)/(-L^2)^(1/2)/(2*H*r^2+2*r-L^2)^(1/2))-const)/L; |
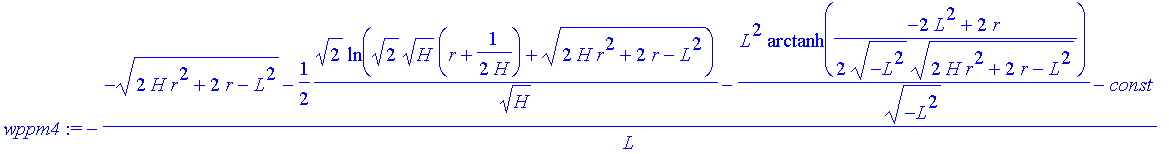
| > |
| > |
| > |
Wir kontrollieren zunächst wieder die zugehörigen Wellenfronten.
Fronten zu Ellipsenbahnen
| > | H:=-0.1: L:=2: |
| > | wellim:=polarplot({seq([r,evalc(Re(wppm4)),r=0..r2+1], |
| > | const=seq(i*L*Pi/4,i=0..7))},scaling=constrained,color=black): |
| > | wellim; |
![[Maple Plot]](wiwe2/wiwe2_1049.gif)
| > | display({welli,wellim,elli}); |
![[Maple Plot]](wiwe2/wiwe2_1050.gif)
| > |
Hyperbelbahnen
| > | H:=0.2: L:=2: # warum dauert das so lang? mit evalf geht es schneller # läuft wieder mit R5 (H>0) |
| > | const:='const': |
| > | # hier braucht man wieder den Realteil |
| > | wppmf:=evalf(Re(wppm)): |
| > |
| > | whypm:=polarplot({seq([r,wppmf,r=r1..15], |
| > | const=seq(i*L*Pi/4,i=0..7))},scaling=constrained,color=blue): |
| > | whypm; |
![[Maple Plot]](wiwe2/wiwe2_1051.gif)
| > |
| > | display({whyp,whypm}); |
![[Maple Plot]](wiwe2/wiwe2_1052.gif)
| > | display({whyp,whypm,hyp}); |
![[Maple Plot]](wiwe2/wiwe2_1053.gif)
Nun können wir die zugehörigen Wellen überlagern. Nachdem die Ausdrücke für die Wirkungsfunktionen aber recht umfangreich sind, wollen wir Maple die Arbeit erleichtern. Die resultierende Welle hat die die Form
| > | z:=exp(I*('wr+L*phi-H*t'))+exp(I*('-wr+L*phi-H*t')); |
![]()
oder
| > | z:=exp(I*(a+b))+exp(I*(-a+b)); |
![]()
Wobei a für der Radialteil der charakteristischen Funktion steht. Dann ist das Absolutquadrat:
| > | az:=z*conjugate(z); |
![]()
Das läßt sich so vereinfachen:
| > | evalc(az); |
![]()
![]()
| > | expand(%); |
![]()
| > | simplify(%); |
![]()
Das ist ein bemerkenswertes Ergebnis! Die azimuthale Abhängigkeit kommt im Amplitudenquadrat nicht mehr vor und die Superposition der aufsteigenden und der absteigenden Wellen läßt sich einfach durch
| > | H:='H': L:='L': |
| > | wres:=cos(evalc(Re(wr)))^2: |
| > | wrf:=evalf(wres): |
beschreiben. (Bei Ellipsenbahnen müssen wir Maple wieder mitteilen, daß wr reell ist)
| > | #wrf; |
| > |
| > | H:=-0.1: L:=0.01: r1;r2;Lm; |
![]()
![]()
![]()
| > | plot3d([r*cos(phi),r*sin(phi),wrf],r=r1..r2+2,phi=0..2*Pi,orientation=[45,17],axes=boxed); |
![[Maple Plot]](wiwe2/wiwe2_1064.gif)
| > |
Schnitt in radialer Richtung
| > | plot(wrf,r=0..r2+2); |
![[Maple Plot]](wiwe2/wiwe2_1065.gif)
| > |
Das ist also schon so etwas wie die Radialverteilung ("s-Zustand" für L=0.01) .. nur fehlt noch die richtige Normierung, was man am Verlauf der Kurve für r>r2 sieht. Aber anstatt unsere "Atomphysik mit einfachen Mitteln" in quantitativer Hinsicht zu überfordern, wollen wir noch ein bißchen Heuristik treiben und die Wellen laufen lassen.
| > | H:='H':L:='L': |
| > | wr; |

Zunächst die Darstellung des Realteils von wr ... für passendes L
| > | L:=1:H:=-0.1: |
| > | plot3d([r*cos(phi),r*sin(phi),cos(evalc(Re(wr)))*cos(L*phi)],r=r1..r2,phi=0..2*Pi,orientation=[45,17],axes=boxed); |
![[Maple Plot]](wiwe2/wiwe2_1067.gif)
| > | #L;phi; |
(radialer Schnitt)
| > | #plot(cos(evalc(Re(wr))),r=r1..r2); |
| > |
Die Animation lohnt sich!!!
| > | n:=20:H:=-0.1: |
| > | animate3d([r*cos(phi),r*sin(phi),cos(evalc(Re(wr)))*cos(L*phi-H*t)],r=r1..r2,phi=0..2*Pi,t=0..2*Pi/abs(H)*(1-1/n), |
| > | style=wireframe,axes=boxed,frames=n,orientation=[30,7]); |
![[Maple Plot]](wiwe2/wiwe2_1068.gif)
| > |
Das macht also ein p-Elektron (L=1). Wie ändert sich das Verhalten des Elektrons mit L und H?
(Für die Berechnung der Ellipsenwellen benötigt man evalc(Re(wr)). Das bremst aber die Berechnung der (in jedem Fall reellen) wr-Werte bei den Hyperbelbahnen ungeheuer. Letztere laufen mit wr alleine nicht mehr in Maple 6.)
| > | n:=20:H:=0.2: |
| > | # Realteil! |
| > | animate3d([r*cos(phi),r*sin(phi),cos(Re(wr))*cos(L*phi-H*t)],r=r1..15,phi=0..2*Pi,t=0..2*Pi/abs(H)*(1-1/n), |
| > | style=wireframe,axes=boxed,frames=n,orientation=[30,7]); |
![[Maple Plot]](wiwe2/wiwe2_1069.gif)
| > |
| > |
Laufen Wirkungswellen bei gebundener Bewegung nach innen und bei ungebundener nach außen?
| > |
komma@oe.uni-tuebingen.de