wiwurf_10.html

wiwurf_10.mws

Moderne Physik mit Maple

PDF-Buch Moderne Physik mit Maple

Update auf Maple 10

Kapitel 5.2.1

Worksheet wiwurf_10.mws

c International Thomson Publishing 1995 filename: wiwurf

Autor: Komma Datum: Oktober 94

Thema: Wirkungswellen beim Wurf

Wirkungswellen am Beispiel des Wurfes (senkrecht und schief)

> restart;with(plots):

Senkrechter Wurf

Wir benötigen den Impuls, die kinetische Energie und die Lagrangefunktion als Funktionen der Gesamtenergie H und der Höhe y.

Energie-Impuls-Beziehung:

> Ep:=p^2/(2*m)=T;

Ep := 1/2*p^2/m = T

Energieerhaltung:

> Ees:=H=T+V;

Lagrange-Funktion:

> Lagr:=L=T-V;

potentielle Energie

> V:=m*g*y;

> sol:=solve({Ep,Ees,Lagr},{p,T,L});

$sol := {T = H-m*g*y, L = H-2*m*g*y, p = RootOf(_Z^2-2*m*H+2*m^2*g*y,label = _L1)}$

> allvalues(%);

> assign(sol);

> allvalues(p);

${T = H-m*g*y, L = H-2*m*g*y, p = (2*m*H-2*m^2*g*y)^(1/2)}, {T = H-m*g*y, L = H-2*m*g*y, p = -(2*m*H-2*m^2*g*y)^(1/2)}$

> py:=op(1,[%]);

>

Senkrechter Wurf mit der Gesamtenergie H und der Fallbeschleunigung g.

charakteristische Funktion:

> w:=int(py,y);

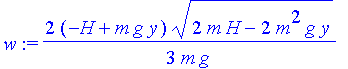
w := 2/3*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g

Ortsabhängiger Teil der Wirkungswelle und ihr Realteil

> psi:=exp(I*w);

psi := exp(2/3*I*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g)

> pr:=Re(psi):

Darstellung des Realteils

> m:=1/2:g:=10:H:=50: ys:=H/(m*g);

> plr:=plot(evalc(pr),y=0..15,numpoints=1000):

> plr;

[Maple Plot]

>

Zunächst erkennt man den Zusammenhang großer Impuls - kleine Wellenlänge. Oberhalb der klassischen Steighöhe ys = H/(m*g) verschwindet die Amplitude aber nicht. Der Impuls wird dort imaginär, und das hat ein exponentielles Abklingen der Amplitude zur Folge: Tunneleffekt!

>

Imaginärteil

> pli:=plot(evalc(Im(psi)),y=0..15,numpoints=1000,color=green):

> pli;

[Maple Plot]

Er verschwindet oberhalb ys und ist unterhalb ys um 90° phasenverschoben, wie es sich gehört!

Wirklich?

plot(evalc(Im(psi)),y=9.99..10.01,color=red);

Gemeinsame Darstellung

> display({plr,pli});

[Maple Plot]

3d-Darstellung des Realteils:

> plot3d(evalc(pr),x=0..1,y=0..15,axes=boxed,grid=[10,100],orientation=[-40,10]);

[Maple Plot]

>

Interferenz der aufsteigenden mit der absteigenden Welle.

Wenn die Wirkungswellen echte Wellen sind, muß sich wegen der "Reflexion" im Scheitelpunkt eine stehende Welle ergeben, allerdings mit ortsabhängiger Wellenlänge. Im Gegensatz zu den gewohnten Wellen können wir aber die Laufrichtung nicht durch das Vorzeichen von Ht umkehren, denn es gilt immer S=W-Ht (und nie S=W+Ht). Die Laufrichtung wird vielmehr durch den Impulsvektor bestimmt, der im eindimensionalen Fall das Vorzeichen von W ändert. Das ist unterhalb des Scheitels unproblematisch. Aber oberhalb des Scheitels wir w imaginär positiv.

> w;

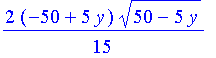
2/15*(-50+5*y)*(50-5*y)^(1/2)

> m:=1/2:g:=10:H:=50:

> plot({w,Im(w)},y=-ys..2*ys);

[Maple Plot]

>

Wir dürfen also oberhalb von ys das Vorzeichen nicht ändern, sonst bekommen wir eine unphysikalische (exponentiell ansteigende) Lösung.

> m:='m':g:='g':H:='H':t:='t':ys:='ys':

> Sp:=w-H*t;

Sp := 2/3*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g-H*t

Herausfiltern des unphysikalischen Teils mit conjugate

> Sm:=-conjugate(w)-H*t;

Sm := -2/3*conjugate((-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g)-H*t

Interferenz

> psiint:=exp(I*Sp)+exp(I*Sm);

psiint := exp((2/3*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g-H*t)*I)+exp((-2/3*conjugate((-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g)-H*t)*I)

Steighöhe (kann in Bereichsangaben von Plotbefehlen verwendet werden)

> ys:=H/(m*g);

ys := H/m/g

Realteil der stehenden Welle

> t:='t':

> rpsiint:=evalc(Re(psiint));

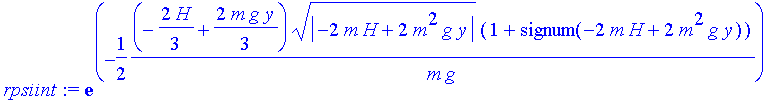
rpsiint := exp(-1/2*(-2/3*H+2/3*m*g*y)*abs(-2*m*H+2*m^2*g*y)^(1/2)*(1+signum(-2*m*H+2*m^2*g*y))/m/g)*cos(-1/2*(-2/3*H+2/3*m*g*y)*abs(-2*m*H+2*m^2*g*y)^(1/2)*(1-signum(-2*m*H+2*m^2*g*y))/m/g+H*t)+exp(-1...

> m:=1/2:g:=10:H:=50:t:=0.01:

> plot(rpsiint,y=-5..12,a=-2..2,numpoints=1000);

[Maple Plot]

>

Eine Momentaufnahme steht natürlich. Aber steht auch die Welle?

> t:='t':

> animate(rpsiint,y=0..12,t=0..2*Pi/H,numpoints=500);

[Maple Plot]

>

Realistischer als die unendlich ausgedehnten Wellen ist ein halbwegs lokalisiertes Teilchen, das den Umkehrpunkt zur Zeit t = 0 erreicht. Wir brauchen zur Simulation der Reflexion zwei davon:

Reflexion = Überlagerung zweier gegenläufiger Pakete (jenseits des Umkehrpunktes werden die Pakete durch die Amplitude der Wirkungswelle automatisch ausgeblendet s.u.).

Test der Paketfunktionen

> m:='m':g:='g':H:='H':y01:='y01':y02:='y02':t:='t':s:='s':ys:='ys':

Paketmittelpunkte

> y01:=ys+1/2*g*t^2;

y01 := ys+1/2*g*t^2

> y02:=ys-1/2*g*t^2;

y02 := ys-1/2*g*t^2

> paket1:=exp(-(y-y01)^2/s^2);

paket1 := exp(-(y-ys-1/2*g*t^2)^2/s^2)

> paket2:=exp(-(y-y02)^2/s^2);

paket2 := exp(-(y-ys+1/2*g*t^2)^2/s^2)

> total:=paket1+paket2;

total := exp(-(y-ys-1/2*g*t^2)^2/s^2)+exp(-(y-ys+1/2*g*t^2)^2/s^2)

>

> ys:=H/m/g;

ys := H/m/g

>

> m:=1/2:g:=10:H:=50:s:=2:

> total;

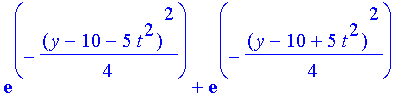
exp(-1/4*(y-10-5*t^2)^2)+exp(-1/4*(y-10+5*t^2)^2)

> animate(total,y=-ys..2*ys,t=-2..2,frames=100,numpoints=500);

[Maple Plot]

>

In diese Einhüllenden setzen wir die Wirkungswellen von oben

> m:='m':g:='g':H:='H':s:='s':

> Sp:=w-H*t;

Sp := 2/3*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g-H*t

> Sm:=-conjugate(w)-H*t;

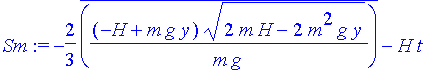
Sm := -2/3*conjugate((-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g)-H*t

Interferenz (nach Multiplikation mit den Paketfunktionen)

> psiint:=exp(I*Sp)*paket1+exp(I*Sm)*paket2;

psiint := exp((2/3*(-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g-H*t)*I)*exp(-(y-H/m/g-1/2*g*t^2)^2/s^2)+exp((-2/3*conjugate((-H+m*g*y)*(2*m*H-2*m^2*g*y)^(1/2)/m/g)-H*t)*I)*exp(-(y-H/m/g+1/2*g*t^2)^2/s^2)

> rpsiint:=evalc(Re(psiint));

Bitte warten ...

> m:=1/2:g:=10:H:=50:s:=3:

> animate(rpsiint,y=-ys..2*ys,t=-2..2,numpoints=400,frames=100);

[Maple Plot]

>

Die Sache klappt also im Prinzip für den senkrechten Wurf, d.h. wir haben soeben mit geringem Aufwand die "WKB-Näherung für das im Schwerefeld tanzende Elektron" erzeugt und sichtbar gemacht!

Schiefer Wurf

Für den schiefen Wurf müssen wir in x-Richtung eine Bewegung mit konstantem Impuls px überlagern

> m:='m':g:='g': H:='H':px:='px':V:='V':

> ys:=(H-1/2*px^2/m)/m/g;

ys := (H-1/2*px^2/m)/m/g

> py:=sqrt(2*m*(H-V)-px^2);

> V:=m*g*y;

> w:=int(py,y)+px*x;

w := -1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)+px*x

Zur Kontrolle die Bahn, die man aus der Wirkungsfunktion am einfachsten so erhält:

> ypl:=diff(w,px);

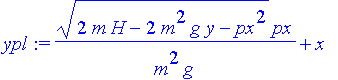
ypl := 1/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(1/2)*px+x

> ypl:=solve(ypl,y);

ypl := -1/2*(-2*m*H*px^2+px^4+x^2*m^4*g^2)/m^2/g/px^2

> m:=1/2:g:=10:H:=50:px:=2:

> plot(ypl,x=-8..8);

[Maple Plot]

(Ende Bahn)

> m:='m':g:='g': H:='H':px:='px':

> #w;

> rpsiS:=evalc(Re(exp(I*(w-H*t))));

rpsiS := exp(1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*sin((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*Pi))*cos(-1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*cos((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*...

> #ys;

Im Gegensatz zum senkrechten Wurf müssen wir jetzt im Umkehrpunkt die Wellenfronten wechseln, die zu positivem bzw. negativem py gehören. Hier sind z.B. die Wirkungswellen zum aufsteigenden Ast (py positiv)

> px:=6:H:=50:g:=10:m:=1/2:n:=40:

> animate3d(rpsiS,x=0..2,y=0..1.5*ys,t=0..2*Pi/H*(1-1/n),axes=boxed,grid=[50,20],orientation=[-40,20],frames=n,style=wireframe);

[Maple Plot]

>

> animate3d(rpsiS,x=0..2,y=0..1.5*ys,t=0..2*Pi/H*(1-1/n),axes=boxed,grid=[50,20],orientation=[-40,20],frames=n,style=patchcontour);

[Maple Plot]

>

Man darf sich vom Bild nicht täuschen lassen: Wenn Sie die Parameter ändern, werden Sie feststellen, daß die Wellen unerwartete Muster aufweisen können. Das liegt an der Interpolation, die von den Maple-Plotroutinen gemacht wird, also auch an der Orientierung von 3d-Plots. In solchen Fällen muß man die Auflösung erhöhen oder ändern (grid), bzw. einen Contourplot erstellen.

> t:=0:px:=6:

> contourplot(rpsiS,x=0..2,y=0..1.5*ys,axes=boxed,grid=[60,50],contours=5);

[Maple Plot]

>

Ein altes Problem des Übergangs von der klassischen Physik zu Quantenphysik, mit dem sich schon Schrödinger und Sommerfeld geplagt haben, ist: wie sind die Randbedingungen bzw. Anfangsbedingungen zu wählen? In der Quantenmechanik = Wellenmechanik gibt es keine wirkliche Bahn mehr. Es gibt nur noch Erhaltungsgrößen. Ein Zustand wird durch Interferenz gebildet. Aber Interferenz wovon? Fällt das Teilchen gerade oder steigt es? (Es macht zu jeder Zeit beides.) Von wo aus steigt es oder fällt es? Welcher Ast der (mindestens zweiwertigen) Funktion der Wellenfronten ist zu nehmen? Diese Fragen führen im Falle der periodischen Bewegungen zu den Wirkungs- und Winkelvariablen. In unserem Beispiel des schiefen Wurfes (aperiodischer Grenzfall = Parabel) können wir diesen Überlegungen schon fast spielerisch nachgehen.

>

Schiefer Wurf mit Interferenz

> m:='m':g:='g': H:='H':px:='px':t:='t':w;s:='s':ys:='ys':

-1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)+px*x

Wir lassen wieder zwei Pakete gegen den Umkehrpunkt laufen (und darüber hinaus):

> y01:=ys+1/2*g*t^2*signum(t);

y01 := ys+1/2*g*t^2*signum(t)

> y02:=ys-1/2*g*t^2*signum(t);

y02 := ys-1/2*g*t^2*signum(t)

> ys:=(H-1/2*px^2/m)/m/g;

ys := (H-1/2*px^2/m)/m/g

> paket1:=exp(-((y-y01)^2+(x-px/m*t)^2)/s^2);

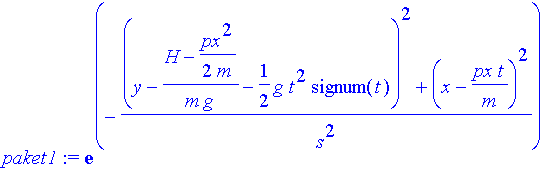
paket1 := exp(-((y-(H-1/2*px^2/m)/m/g-1/2*g*t^2*signum(t))^2+(x-px/m*t)^2)/s^2)

> paket2:=exp(-((y-y02)^2+(x-px/m*t)^2)/s^2):

Für die Plots ist es ganz günstig, wenn wir die Steigzeit und die Wurfweite zur Verfügung haben:

> ts:=sqrt(2*ys/g);

ts := 2^(1/2)*((H-1/2*px^2/m)/m/g^2)^(1/2)

> xw:=abs(px)/m*ts;

xw := abs(px)/m*2^(1/2)*((H-1/2*px^2/m)/m/g^2)^(1/2)

Nun noch die charakteristischen Funktionen

> wp:=w;

wp := -1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)+px*x

> wm:=conjugate(-w)+2*px*x;

wm := conjugate(1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)-px*x)+2*px*x

Und die Amplituden der Wirkungswellen

> rpsip:=evalc(Re(exp(I*wp)));

rpsip := exp(1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*sin((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*Pi))*cos(-1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*cos((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*...

> rpsim:=evalc(Re(exp(I*wm)));

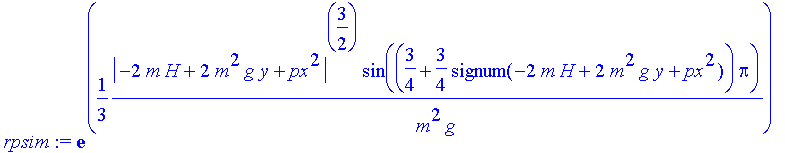
rpsim := exp(1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*sin((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*Pi))*cos(1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*cos((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*P...

>

Kontrollplots

m:=1/2:g:=10:H:=50:

px:=2:

t:=0:s:=2:

rpsim;

plot3d(rpsip,x=-xw..xw,y=0..2*ys,axes=boxed,grid=[50,50],orientation=[-90,0],style=contour,contours=4);

plot3d(rpsim,x=-xw..xw,y=0..2*ys,axes=boxed,grid=[50,50],orientation=[-90,0],style=contour,contours=5);

m:='m':g:='g':H:='H':px:='px':t:='t':s:='s':

Wirkungsfunktionen, zeitabhängig

> Sp:=wp-H*t;

Sp := -1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)+px*x-H*t

> Sm:=wm-H*t;

Sm := conjugate(1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)-px*x)+2*px*x-H*t

Interferenz

> wurf:=paket1*exp(I*Sp)+paket2*exp(I*Sm);

wurf := exp(-((y-(H-1/2*px^2/m)/m/g-1/2*g*t^2*signum(t))^2+(x-px/m*t)^2)/s^2)*exp((-1/3/m^2/g*(2*m*H-2*m^2*g*y-px^2)^(3/2)+px*x-H*t)*I)+exp(-((y-(H-1/2*px^2/m)/m/g+1/2*g*t^2*signum(t))^2+(x-px/m*t)^2)/...

Realteil

> Rwurf:=evalc(Re(wurf));

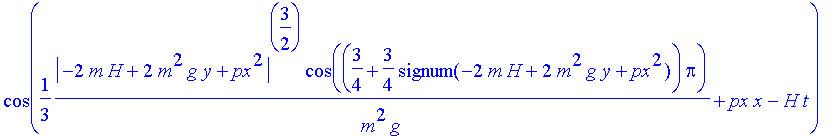
Rwurf := exp((-(y-H/m/g+1/2/m^2/g*px^2-1/2*g*t^2*signum(t))^2-(x-px/m*t)^2)/s^2)*exp(1/3*1/m^2/g*abs(-2*m*H+2*m^2*g*y+px^2)^(3/2)*sin((3/4+3/4*signum(-2*m*H+2*m^2*g*y+px^2))*Pi))*cos(-1/3*1/m^2/g*abs(-...

Zahlenwerte

> m:=1/2:g:=10:H:=50:

> px:=2:

> t:=-1/2*ts:s:=2:

Alle Parameter gesetzt?

> #Rwurf;

Momentaufnahme

> plot3d(Rwurf,x=-xw..xw,y=0..2*ys,axes=boxed,grid=[50,50],orientation=[-90,0],style=contour,contours=5);

[Maple Plot]

> plot3d(Rwurf,x=-xw..xw,y=0..2*ys,axes=boxed,grid=[50,20],orientation=[-40,2],style=wireframe);

[Maple Plot]

>

Animation

> n:=40:t:='t':s:=2:px:=1:#Digits:=2: ändert nichts an Geschwindigkeit und Interpolation

Bitte warten ... oder kleineres n wählen

> animate3d(10^10*Rwurf,x=-xw-s..xw+s,y=0..1.5*ys,t=-ts..ts,axes=boxed,orientation=[-90,0],grid=[50,50],frames=n,style=contour,shading=z,contours=5);

[Maple Plot]

>

Leider Interpolationsfehler bei linearer Darstellung (ln(10+Rwurf) bzw. Quadrieren beheben das, beseitigen aber auch die interessanten Wellenfronten S=0, auf denen das Teilchen zu reiten scheint -- mit stroboskopischen Effekten. Quadrat (od. gerade Hochzahl) hat unerwünschten Nebeneffekt im Scheitel, weil Max u. Min. gleich bewertet werden).

Man kann aber mit 10^10 multiplizieren (dann aber nicht 1:1 wählen), um die Interpolationskreuze zum Verschwinden zu bringen (10^6 tut es nicht).

Abb.p5..7wiwurf.ps Postscript-Fans können jetzt ihre ps-files am laufenden Band produzieren:

t:='t':vxlab:=``:

for t from -1 to 1 do

vtitle:=`t=`.t: `Name`:=p.(6+t).wiwurf.`.`.ps:pspl(Name):

plot3d(10^10*Rwurf,x=-xw-s..xw+s,y=0..1.5*ys,axes=framed,orientation=[-90,0],grid=[100,100],style=contour,shading=z,contours=5,opt3d);winpl():

od;

>

> n:=50:t:='t':

> animate3d(Rwurf,x=-xw-s..xw+s,y=0..1.5*ys,t=-ts..ts,axes=boxed,frames=n,grid=[20,20],orientation=[-40,55],style=wireframe,scaling=constrained);

[Maple Plot]

>

Wir treiben die *Simulation* noch einen Schritt weiter und lassen das Teilchen entstehen und vergehen:

> s:=1+abs(t);

Bitte warten, bis das Teilchen entstanden ist ...

> n:=20:

> animate3d(10^10*Rwurf,x=-xw-2..xw+2,y=0..1.5*ys,t=-ts..ts,axes=boxed,orientation=[-90,0],grid=[50,50],frames=n,style=contour,shading=z,contours=5);

[Maple Plot]

Während das Elektron im Scheitel eine Schrödingersche Zitterbewegung macht, taucht unten Diracs See auf ... verkehrte Welt.

>

Amplitude umgekehrt proportional zur Zeit

> n:=100:

> animate3d(Rwurf/s,x=-xw-3..xw+3,y=0..1.5*ys,t=-ts..ts,frames=n,grid=[30,20],orientation=[-65,65]);

[Maple Plot]

>

komma@oe.uni-tuebingen.de