schroesolve.html

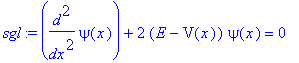
Geschlossene Lösungen der SGL für verschiedene Potentiale

SGL in "natürlichen Einheiten" m = h = e =...= 1.

`>`	*sgl := diff(psi(x),x$2)+2(E - V(x))psi(x)=0;*

sgl := diff(psi(x),`$`(x,2))+2*(E-V(x))*psi(x) = 0

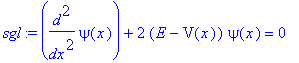
`>`	dsolve(sgl,psi(x));

$psi(x) = DESol({(2*E-2*V(x))*_Y(x)+diff(_Y(x),`$`(x,2))},{_Y(x)})$

>

Ohne konkretes Potential nur ein Platzhalter für die Lösung.

`>`	DEtools[odeadvisor](sgl);

>

Konstantes Potential (im Topf)

`>`	V:=x->const;

`>`	dsolve(sgl,psi(x));

Das hätte man zur Not auch noch von Hand ausrechnen können :-))

Fallunterscheidungen

>

`>`	V:=x->-2: E:=-1:

`>`	dsolve(sgl,psi(x));

`>`	E:=-5:

`>`	dsolve(sgl,psi(x));

>

Oszillator

`>`	E:='E': V:=x->x^2/2;

`>`	dsolve(sgl,psi(x));

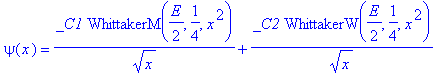
psi(x) = _C1/x^(1/2)*WhittakerM(1/2*E,1/4,x^2)+_C2/x^(1/2)*WhittakerW(1/2*E,1/4,x^2)

Die Whittaker-Funktionen sind eine Verallgemeinerung der hypergeometrischen Funktionen.

`>`	convert(rhs(%),hypergeom);

_C1/x^(1/2)/exp(1/2*x^2)*(x^2)^(3/4)*hypergeom([3/4-1/2*E],[3/2],x^2)+_C2/x^(1/2)/exp(1/2*x^2)*Pi^(1/2)*((x^2)^(1/4)/GAMMA(3/4-1/2*E)*hypergeom([1/4-1/2*E],[1/2],x^2)-2*(x^2)^(3/4)/GAMMA(1/4-1/2*E)*hyp...

`>`	simplify(%);

-(x^2)^(1/4)*(-_C1*csgn(x)*x*hypergeom([3/4-1/2*E],[3/2],x^2)*GAMMA(3/4-1/2*E)*GAMMA(1/4-1/2*E)-_C2*Pi^(1/2)*hypergeom([1/4-1/2*E],[1/2],x^2)*GAMMA(1/4-1/2*E)+2*_C2*Pi^(1/2)*csgn(x)*x*hypergeom([3/4-1/...

`>`	convert(%,StandardFunctions);

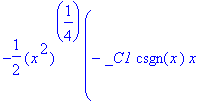
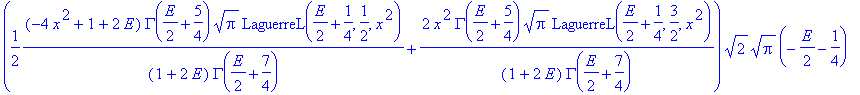
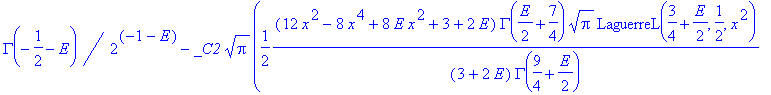
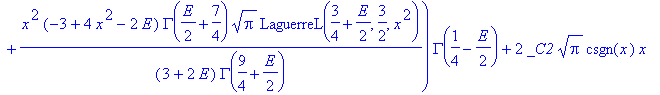
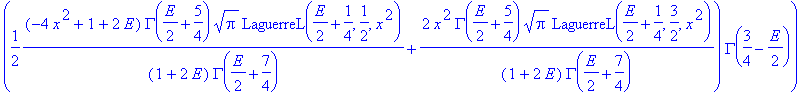
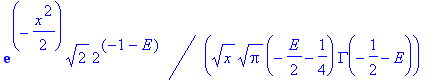
-1/2*(x^2)^(1/4)*(-_C1*csgn(x)*x*(1/2*(-4*x^2+1+2*E)/(1+2*E)/GAMMA(1/2*E+7/4)*GAMMA(1/2*E+5/4)*Pi^(1/2)*LaguerreL(1/2*E+1/4,1/2,x^2)+2*x^2/(1+2*E)/GAMMA(1/2*E+7/4)*GAMMA(1/2*E+5/4)*Pi^(1/2)*LaguerreL(1...

`>`	#simplify(%);

>

Also ein Spaziergang durch die speziellen Funktionen der mathematischen Physik...

>

Für konkrete Eigenwerte, erhält man die gewohnten Funktionen

>

`>`	E:=1/2:

`>`	dsolve(sgl,psi(x));

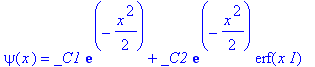
psi(x) = _C1*exp(-1/2*x^2)+_C2*exp(-1/2*x^2)*erf(x*I)

Anfangsbedingungen (müssen zu den EW passen - gerade, ungerade):

`>`	dsolve({sgl,psi(0)=1,D(psi)(0)=0},psi(x));

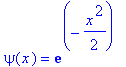
psi(x) = exp(-1/2*x^2)

`>`	E:=9/2:

`>`	dsolve(sgl,psi(x));

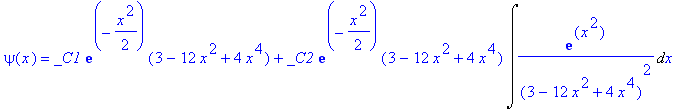
psi(x) = _C1*exp(-1/2*x^2)*(3-12*x^2+4*x^4)+_C2*exp(-1/2*x^2)*(3-12*x^2+4*x^4)*Int(1/(3-12*x^2+4*x^4)^2*exp(x^2),x)

`>`	dsolve({sgl,psi(0)=1,D(psi)(0)=0},psi(x));

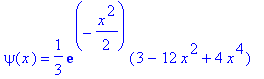
psi(x) = 1/3*exp(-1/2*x^2)*(3-12*x^2+4*x^4)

>

Probe (auch von Hand möglich):

`>`	subs(%,sgl);

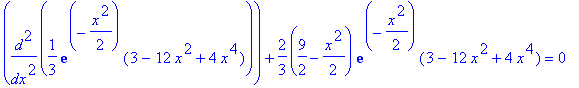
diff(1/3*exp(-1/2*x^2)*(3-12*x^2+4*x^4),`$`(x,2))+2/3*(9/2-1/2*x^2)*exp(-1/2*x^2)*(3-12*x^2+4*x^4) = 0

`>`	simplify(%);

>

`>`	E:='E':

`>`	solosz:=(x,_E)->dsolve({subs(E=_E,sgl),psi(0)=1,D(psi)(0)=0},psi(x));

$solosz := proc (x, _E) options operator, arrow; dsolve({subs(E = _E,sgl), D(psi)(0) = 0, psi(0) = 1},psi(x)) end proc$

`>`	solosz(x,3.4);

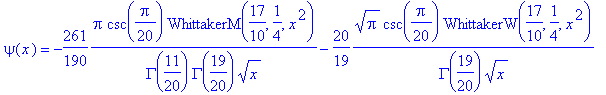
psi(x) = -261/190*Pi*csc(1/20*Pi)/GAMMA(11/20)/GAMMA(19/20)/x^(1/2)*WhittakerM(17/10,1/4,x^2)-20/19*Pi^(1/2)*csc(1/20*Pi)/GAMMA(19/20)/x^(1/2)*WhittakerW(17/10,1/4,x^2)

>

Beliebige Energien

`>`	plot([seq(rhs(solosz(x,E)),E=0..5)],x=0..5,-5..5,thickness=2);

[Maple Plot]

>

Eigenwerte

`>`	*plot([seq(rhs(solosz(x,E)),E=seq(2n+1/2,n=0..5))],x=0..5,-2..2,thickness=2);**

[Maple Plot]

Normierung immer mit Integration möglich

`>`	int(rhs(solosz(x,9/2))^2,x=0..infinity);

>

Oder gleich mit den bekannten Funktionen

`>`	*u:=(n,x)->1/sqrt(2^nn!)Pi^(-1/4)HermiteH(n,x)exp(-x^2/2);*

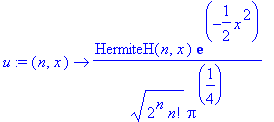
u := proc (n, x) options operator, arrow; 1/sqrt(2^n*n!)/Pi^(1/4)*HermiteH(n,x)*exp(-1/2*x^2) end proc

`>`	seq(simplify(u(n,x)),n=0..5);

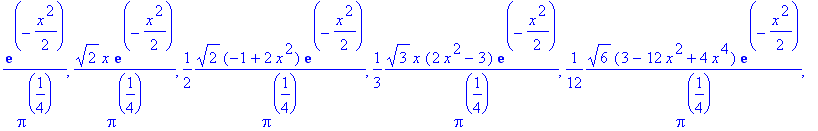
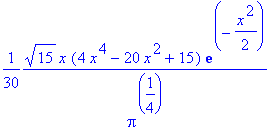
1/Pi^(1/4)*exp(-1/2*x^2), 2^(1/2)/Pi^(1/4)*x*exp(-1/2*x^2), 1/2*2^(1/2)*(-1+2*x^2)*exp(-1/2*x^2)/Pi^(1/4), 1/3*3^(1/2)*x*(2*x^2-3)*exp(-1/2*x^2)/Pi^(1/4), 1/12*6^(1/2)*(3-12*x^2+4*x^4)*exp(-1/2*x^2)/Pi...

>

`>`	plot([seq(u(n,x)+n+1/2,n=0..7),seq(n+1/2,n=0..7),V(x)],x=-5..5,0..10,color=[red,blue]);

[Maple Plot]

>

Coulombpotential

`>`	restart:

`>`	*sgl := diff(psi(x),x$2)+2(E - V(x))psi(x)=0;*

sgl := diff(psi(x),`$`(x,2))+2*(E-V(x))*psi(x) = 0

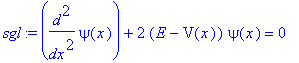
`>`	E:='E': V:=x->-1/sqrt(x^2);

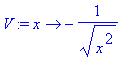
V := proc (x) options operator, arrow; -1/sqrt(x^2) end proc

`>`	dsolve(sgl,psi(x));

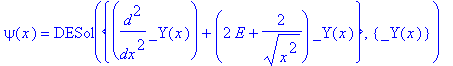
$psi(x) = DESol({diff(_Y(x),`$`(x,2))+(2*E+2/(x^2)^(1/2))*_Y(x)},{_Y(x)})$

So geht es:

`>`	V:=x->-1/x;

`>`	dsolve(sgl,psi(x));

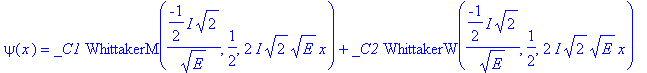
psi(x) = _C1*WhittakerM(-1/2*I*2^(1/2)/E^(1/2),1/2,2*I*2^(1/2)*E^(1/2)*x)+_C2*WhittakerW(-1/2*I*2^(1/2)/E^(1/2),1/2,2*I*2^(1/2)*E^(1/2)*x)

>

E=-1/2/n^2

`>`	E:=-1/2:

`>`	dsolve(sgl,psi(x));

Mit Anfangsbedingungen

`>`	E:=-1/2/4:

`>`	dsolve({sgl,psi(0)=0,D(psi)(0)=1},psi(x));

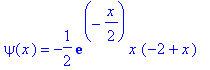
psi(x) = -1/2*exp(-1/2*x)*x*(-2+x)

`>`	#collect(expand(%),exp);

>

Probe (auch von Hand zu empfehlen):

`>`	subs(%,sgl);

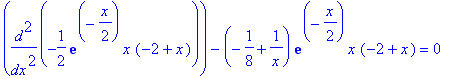
diff(-1/2*exp(-1/2*x)*x*(-2+x),`$`(x,2))-(-1/8+1/x)*exp(-1/2*x)*x*(-2+x) = 0

`>`	simplify(%);

>

`>`	E:=-1/2/9:

`>`	dsolve({sgl,psi(0)=0,D(psi)(0)=1},psi(x));

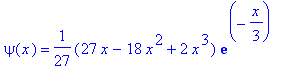
psi(x) = 1/27*(27*x-18*x^2+2*x^3)*exp(-1/3*x)

`>`	collect(expand(%),exp);

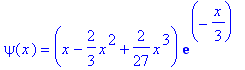
psi(x) = (x-2/3*x^2+2/27*x^3)*exp(-1/3*x)

>

`>`	subs(%,sgl);

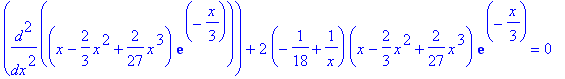
diff((x-2/3*x^2+2/27*x^3)*exp(-1/3*x),`$`(x,2))+2*(-1/18+1/x)*(x-2/3*x^2+2/27*x^3)*exp(-1/3*x) = 0

`>`	simplify(%);

>

Mit den Standardfunktionen

`>`	*La:=(n,l,x)->simplify(LaguerreL(n-l-1,2l+1,x));**

`>`	La(3,1,x);

`>`	#convert(LaguerreL(n,l,x),hypergeom);

`>`	#simplify(%);

`>`	#convert(binomial(l+n,n),`!`);

>

Oder

`>`	l,n,j,k,u:='l','n','j','k','u': *L:=(j,k,u)->if j<>0 then 1/j!exp(u)/u^kdiff(u^(j+k)exp(-u),u$j)**

`>`	else 1 fi;

>

`>`	*#Lt:=(n,l,x)->L(n-l-1,2l+1,x);**

`>`	#La(10,7,x);

`>`	#simplify(Lt(10,7,x));

>

`>`	*Ru:=(n,l,u)->u^lexp(-u/2)L(n-l-1,2l+1,u);**

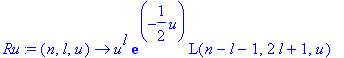
Ru := proc (n, l, u) options operator, arrow; u^l*exp(-1/2*u)*L(n-l-1,2*l+1,u) end proc

`>`	Ru(3,1,u);

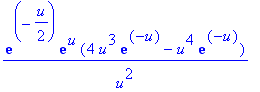
1/u^2*exp(-1/2*u)*exp(u)*(4*u^3*exp(-u)-u^4*exp(-u))

`>`	collect(expand(%),exp);

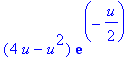
(4*u-u^2)*exp(-1/2*u)

`>`	a0:=1: *plr:=u->subs(u=2r/(na0),simplify(Ru(n,l,u)));*

`>`	#plr(o);

Normierung

`>`	*Nr2:=4(n-l-1)!/(n+l)!/(a0^3n^4); #Normierung^2 (1-dim, 3-dim, s.u.)?*

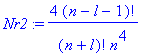
Nr2 := 4*(n-l-1)!/(n+l)!/n^4

`>`	n:=3:l:=0:

`>`	*plot(Nr2r^2plr(o)^2,r=0..40);*

[Maple Plot]

>

`>`	n:='n':l:=0: *plot([seq(Nr2(rplr(o))^2-1/2/n^2,n=1+l..4),seq(-1/2/n^2,n=1+l..4),-1/r],r=0..40,-0.6..0.1,color=[red,blue],tickmarks=[2,2]);*

[Maple Plot]

Lineares Potential (Wurf)

`>`	E:='E': V:=x->x:

>

`>`	dsolve(sgl,psi(x));

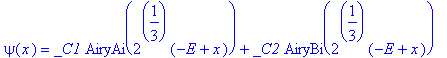
psi(x) = _C1*AiryAi(2^(1/3)*(-E+x))+_C2*AiryBi(2^(1/3)*(-E+x))

Die Airy-Funktionen lassen sich als Besselfunktionen schreiben

`>`	convert(rhs(%),Bessel);

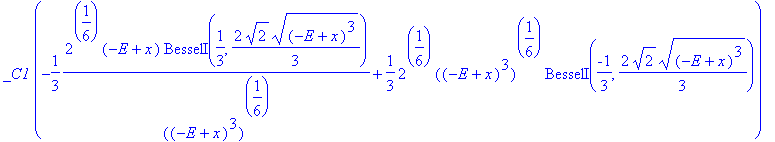
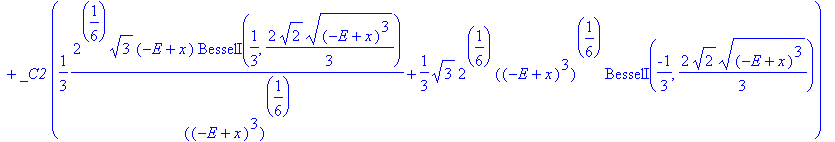
_C1*(-1/3*2^(1/6)/((-E+x)^3)^(1/6)*(-E+x)*BesselI(1/3,2/3*2^(1/2)*((-E+x)^3)^(1/2))+1/3*2^(1/6)*((-E+x)^3)^(1/6)*BesselI(-1/3,2/3*2^(1/2)*((-E+x)^3)^(1/2)))+_C2*(1/3*2^(1/6)*3^(1/2)/((-E+x)^3)^(1/6)*(-...

>

Anfangsbedingungen vereinfachen die Sache nicht wesentlich :-))

`>`	dsolve({sgl,psi(0)=0,D(psi)(0)=1},psi(x));

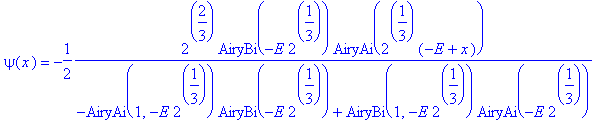
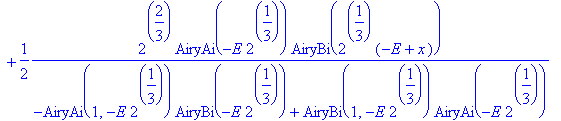
psi(x) = -1/2*2^(2/3)/(-AiryAi(1,-E*2^(1/3))*AiryBi(-E*2^(1/3))+AiryBi(1,-E*2^(1/3))*AiryAi(-E*2^(1/3)))*AiryBi(-E*2^(1/3))*AiryAi(2^(1/3)*(-E+x))+1/2*2^(2/3)*AiryAi(-E*2^(1/3))/(-AiryAi(1,-E*2^(1/3))*...

`>`	simplify(%);

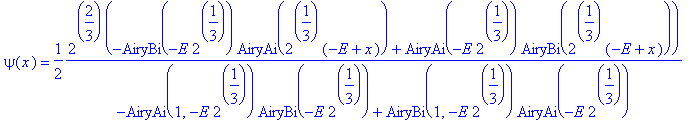
psi(x) = 1/2*2^(2/3)*(-AiryBi(-E*2^(1/3))*AiryAi(2^(1/3)*(-E+x))+AiryAi(-E*2^(1/3))*AiryBi(2^(1/3)*(-E+x)))/(-AiryAi(1,-E*2^(1/3))*AiryBi(-E*2^(1/3))+AiryBi(1,-E*2^(1/3))*AiryAi(-E*2^(1/3)))

`>`	#convert(rhs(%),Bessel);

Leider gehört dieses einfache Potential zu den mathematisch nicht ganz "trivialen Fällen", was die geschlossene Lösung der DGL angeht. Es wird aber bei den Experimenten mit Kondensaten im Schwerefeld oft benötigt...

Siehe auch: Schrödingers Oszillator

Zurück zum Inhalt

komma@oe.uni-tuebingen.de