Wie fängt man elektrisch geladene Teilchen ein?

Das ist nicht ganz einfach, insbesondere wenn man die Teilchen zur Ruhe bringen will!
Deshalb gab es 1989 auch den Nobel Prize in Physics dafür.

Mit statischen Feldern ist das nicht möglich. Man muss vielmehr versuchen, das Teilchen durch passende Ansteuerung der Felder "in der Balance zu halten". Kellner schaffen dieses dynamische Gleichgewicht meist länger als Rodeoreiter.
Auch Wolfgang Paul benutzte ein mechanisches Analogon, um dem erstaunten Publikum seine geniale Idee verständlich zu machen: In einer Paul-Falle verhält sich ein elektrisch geladenes Teilchen ähnlich wie eine Kugel auf einer rotierenden Sattelfläche im Schwerefeld.
Die Ähnlichkeit stimmt auch. Man sollte aber nicht in die Falle tappen, das mechanische Analogon mit der elektrischen Paul-Falle gleichzusetzen.

Wir setzen die Kugel zunächst auf einen ruhenden Sattel, der so gebaut ist, dass die Kugel für y = 0 nicht herunterfällt (labiles Gleichgewicht in y-Richtung). Aber schon bei einer Abweichung des Starpunktes von 10^-8m in y-Richtung führt die Kugel nur zwei Schwingungen aus, bevor sie abstürzt.

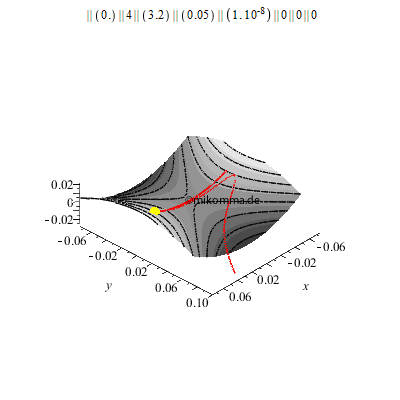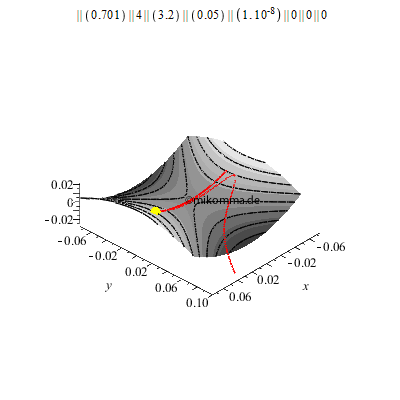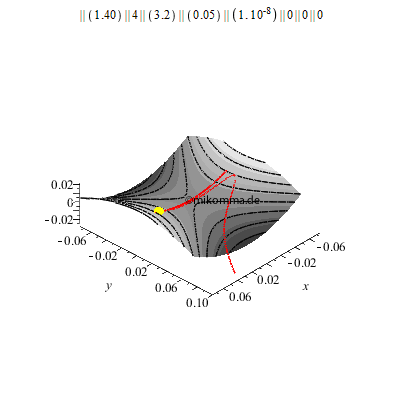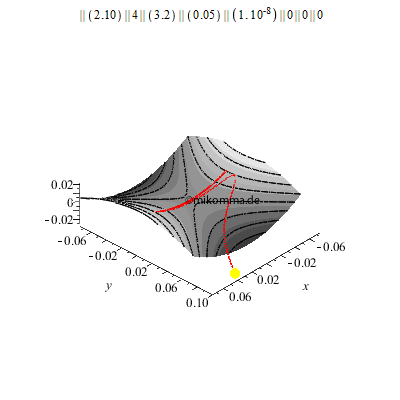
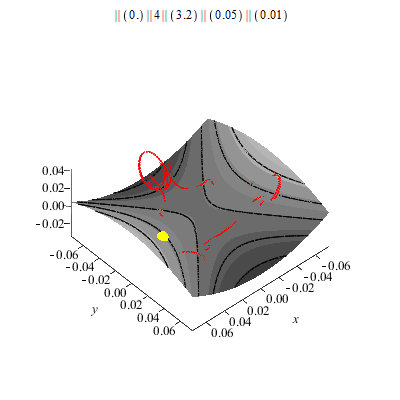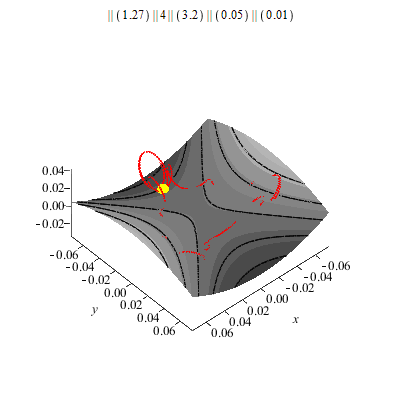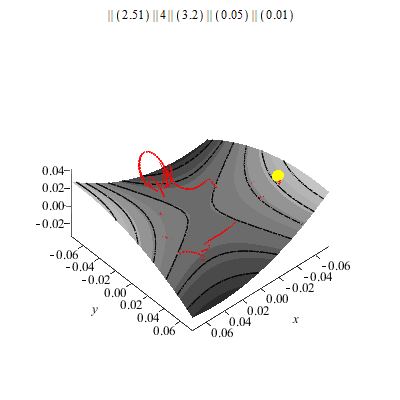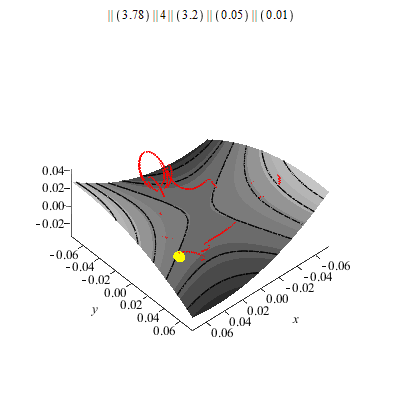
Was macht nun eine Kugel, die unter geeigneten Anfangsbedingungen (Ort und Geschwindigkeit) auf eine rotierende Sattelfläche (geeigneter Form und Winkelgeschwindigkeit) gesetzt wird?

Meistens fliegt sie einfach raus! Es gibt aber "besonders geeignete" Anfangsbedingungen und Formen des Sattels, z.B.:

Sattelform z=a*x^2-b*y^2. Hier a=4, b=3.2, g=10 (MKS-Einheiten). Sieht eigentlich aus wie ein Tischtennisball auf Wasser...

Bei "besonders" geeigneten Anfangsbedingungen schwimmt der Ball auf einem "präzedierenden Dreieck" beliebig lange:

Wie obige Simulationen zeigen ist es theoretisch möglich, eine Kugel auf einer rotierenden Sattelfläche zu balancieren - und es gibt auch Experimente dazu. Aber Vorsicht, es gibt gravierende Unterschiede zur elektrischen Paul-Falle! 1. In der elektrischen Paul-Falle bewegt sich das Teilchen mehr oder weniger auf "Lissajou-Bahnen" (makroskopisch) mit "mikroskopischen" Schwankungen (siehe Abbildung rechts). Der Sattel der elektrischen Paul-Falle (Standard) rotiert nicht. 2. Im Gegensatz zur elektrischen Paul-Falle, bewegt sich ein Teilchen auf dem rotierenden Sattel nicht frei (im Schwerefeld), sondern erfährt Zwangskräfte durch die Sattelfläche (leider anholonom). 3. Im Vergleich zur elektrischen Paul-Falle ist die mechanische hoch chaotisch: Das "präzedierende Dreieck" ist nur ein Beispiel aus Millionen. Man sollte also nicht in diese weit verbreitete Falle tappen: "Ein Teilchen, das sich im (homogenen) Schwerefeld auf einer parabelförmigen Fläche bewegen muss, befindet sich in einem quadratischen Potential"!