Verschränkung | Entanglement
Eine kurze Notiz
Das "eigentliche Geheimnis der Quantenphysik" ist nicht die Superposition von Zuständen, sondern die Verschränkung. Die Superposition kann man in einem Raum mit der Basis {|h>,|v>} (z.B. horizontale oder vertikale Polarisation eines Photons) beschreiben. Für die Verschränkung benötigt man den Produktraum mit {|h>,|v>}⊗{|h>,|v>}. Falls man das Glück hat, zwei Photonen in einem reinen Zustand anzutreffen, lassen sie sich so beschreiben:
| (1) |
Dabei ist z.B. |hv> die Kurzschreibweise für das nicht kommutative Tensorprodukt |h>⊗|v>. In der WWW-Standardliteratur liest man nun: "Ein Zustand ist verschränkt, wenn er sich nicht faktorisieren (separieren) lässt". Aber was passiert, wenn sich der Zustand zahlenmäßig nicht exakt faktorisieren lässt, bzw. was ist das Kriterium für Faktorisierbarkeit? Der Zustand (1) lässt sich faktorisieren (ist ein Produktzustand), wenn für die (komplexen) Koeffizienten gilt:
| (2) |
bzw.
![Typesetting:-mprintslash([det(Matrix([[c11, c12], [c21, c22]])) = 0], [det(Matrix(%id = 18446744075663530574)) = 0])](verschr_3.gif) |
(3) |
Wenn Gleichung (2) (oder (3)) nicht exakt erfüllt ist, ist der Zustand "ein bisschen verschränkt". Wann ist umgekehrt Gleichung (2) maximal verletzt, bzw. gibt es ein Maß für die Verschränkung? Aus der zum Zustand (1) gehörenden Dichtematrix
![Typesetting:-mprintslash([rho := Matrix([[`*`(`^`(abs(c11), 2)), `*`(c11, `*`(conjugate(c12))), `*`(c11, `*`(conjugate(c21))), `*`(c11, `*`(conjugate(c22)))], [`*`(c12, `*`(conjugate(c11))), `*`(`^`(a...](verschr_4.gif) |
(4) |
bildet man die reduzierte Dichtematrix
![Typesetting:-mprintslash([rho1 := Matrix([[`+`(`*`(`^`(abs(c11), 2)), `*`(`^`(abs(c12), 2))), `+`(`*`(c11, `*`(conjugate(c21))), `*`(c12, `*`(conjugate(c22))))], [`+`(`*`(c21, `*`(conjugate(c11))), `*...](verschr_5.gif) |
(5) |
und nimmt (z.B.) als Maß für die Verschränkung die Shannon-Entropie
| (6) |
mit den Eigenwerten λ der reduzierten Dichtematrix (ld dualer Logarithmus).
Für den
Bell-Zustand
c11|hh> + c22|vv>
kann man E über
den
Koeffizienten
c11 und c22
(zunächst
reellwertig)
abtragen: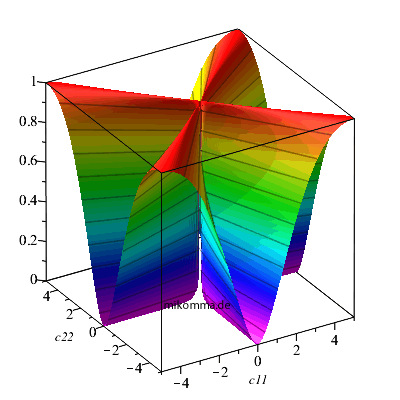 Auf den Winkelhalbierenden ist der Zustand maximal verschränkt (E = 1, rot), auf den Achsen hat man die (einfachsten) Produktzustände (E = 0, violett). Wie bei der Sichtbarkeit von Interferenz gibt es aber auch hier alle Werte zwischen 0 und 1, d.h., "etwas verschränkt" ist der Normalfall. Mit Maple kann man nun bequem mit Schiebern die anderen Koeffizienten in Gleichung (1) einstellen (p11 und p12 sind die Phasen von c11 und c12). Zur Darstellung von E werden die Koeffizienten c normiert, die Zahlen sind also als relatives Maß (oder Gewicht) zu lesen. |
|
Hier sind zwei weitere Beispiele:
|
|
|
Es gibt also wie gesagt nicht nur verschränkte oder nicht verschränkte Zustände, sondern alles dazwischen - von statistischen Gemischen ganz abgesehen...
Zur Veranschaulichung von
![]()
hier noch ein paar Animationen:
1. Ausgehend von einem verschränkten Zustand wie oben (c11|hh> + c22|vv>), kann man weitere Summanden zumischen, z.B. c21=1 und Animation für c12 (reell):
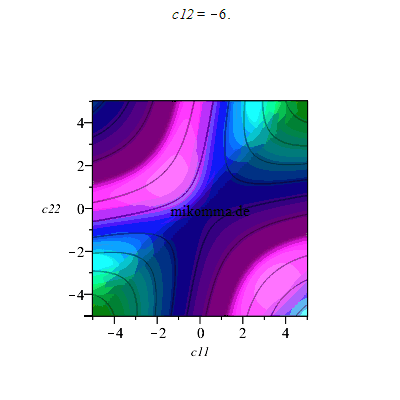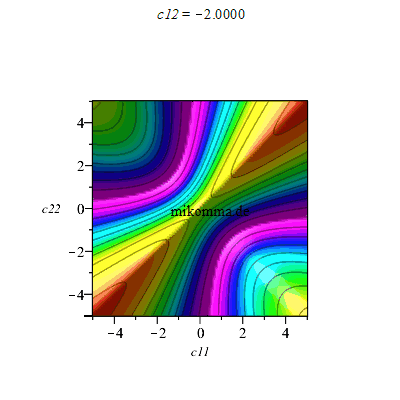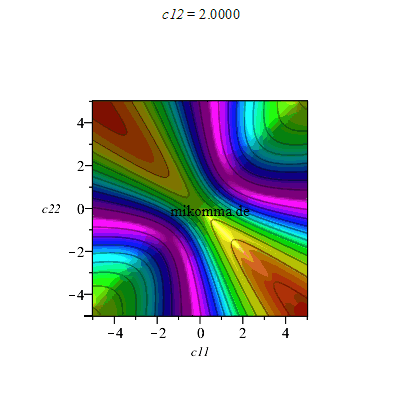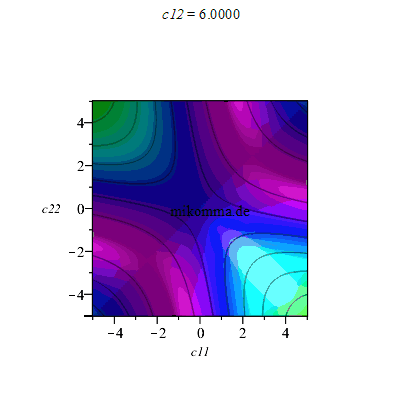 |
Die Produktzustände (E=0) liegen dann auf Hyperbelscharen (violett). Maximale Verschränkung (E=1, rot) wie gehabt auf den Winkelhalbierenden, aber nicht mehr durchgehend.
Aber die Phase spielt auch eine Rolle: c12 = c21 = 1, Animation für p11
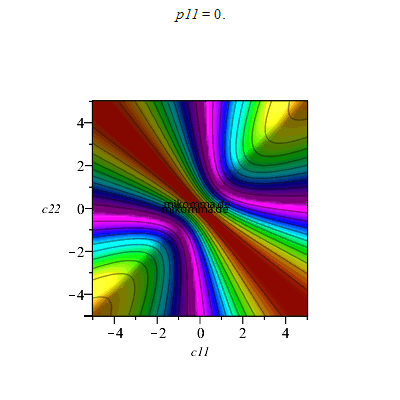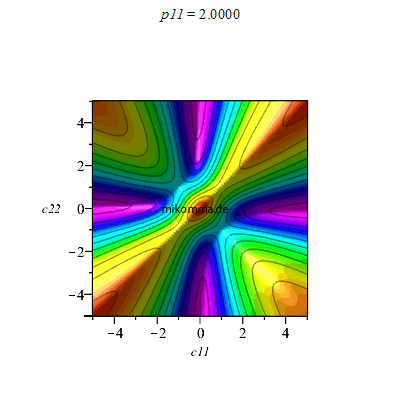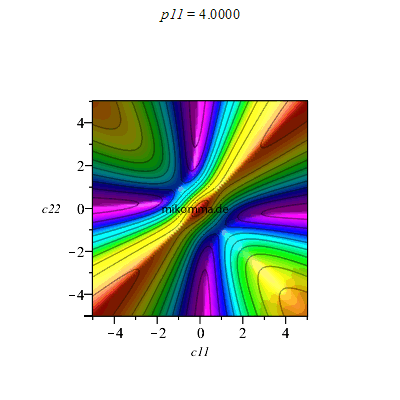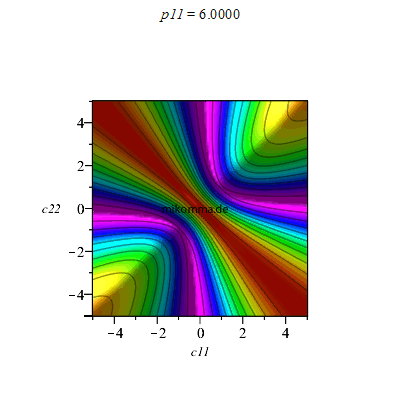 |
2. Ausgehend von einem Produktzustand, z.B. c11|hh> + c12|hv>, und Zumischen der anderen Summanden: c22 = 0.5, Animation für c21
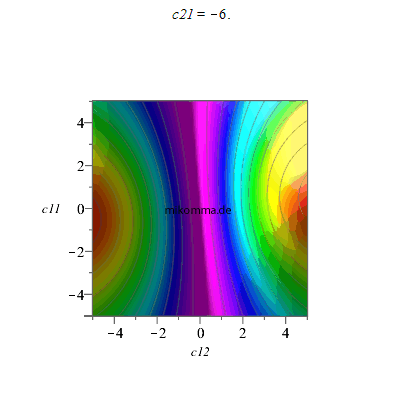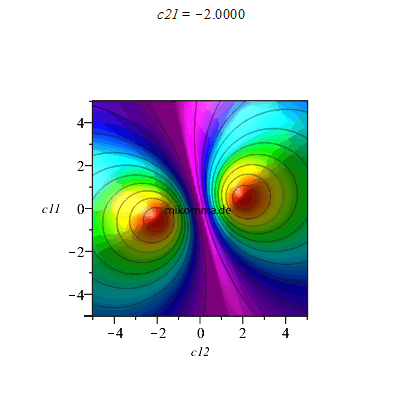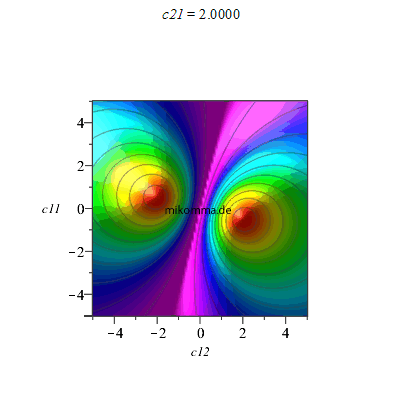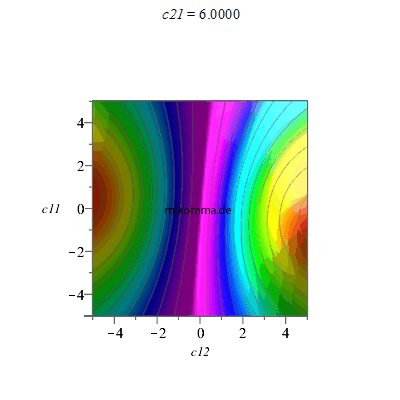 |
Nun liegen die Produktzustände auf Geradenscharen, die von zwei maximal verschränkten Zuständen begleitet werden.
Animation für p11 (p12 = 0, c22 = 1.5, c21 = 2):
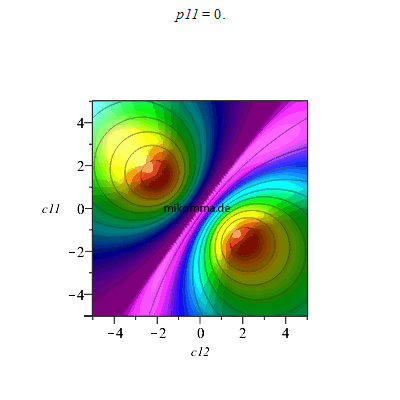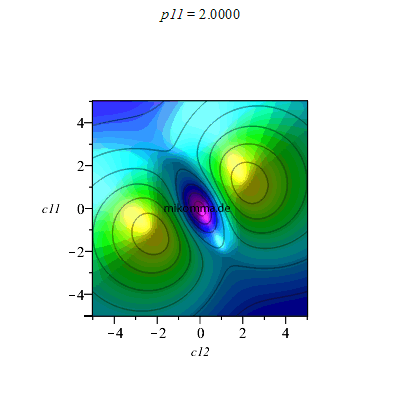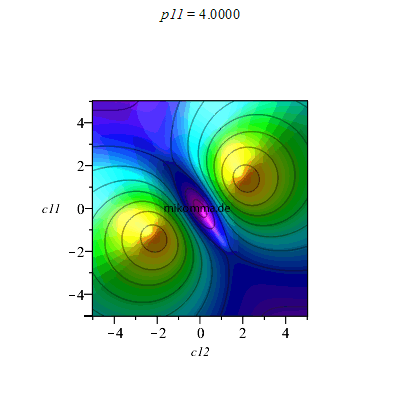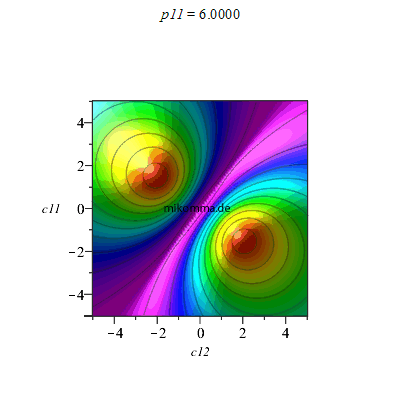 |
So viel zur Theorie. Aber wozu ist das gut? Wenn man es beherrscht, den
Grad der Verschränkung passend einzustellen, kann man "Experimente für die
Geschichtsbücher" machen:
Significant-Loophole-Free Test of Bell’s
Theorem with
Entangled Photons,
DOI:
10.1103/PhysRevLett.115.250401
Nicht zuletzt: Oft wird der Eindruck vermittelt, dass verschränkte Zustände nur im Labor hergestellt ("präpariert") werden können, also in der Natur eigentlich nicht vorkommen, weil sie "höchst fragil" sind und "schnell zerfallen" ("dekohärieren"). Das Gegenteil ist der Fall: separable Zustände (Produktzustände) sind eine Idealisierung, weil es in der Natur keine abgeschlossenen (Sub-) Systeme gibt. So sind z.B. in jedem Atom die Elektronen mit dem Kern und untereinander verschränkt, aber auch die Effizienz der Photosynthese beruht auf Verschränkung - mehr oder weniger.
