Das relativistische Elektron
Genau genommen gibt es kein nichtrelativistisches Elektron. Und genau genommen ist das Elektron nie alleine, denn es hat immer seinen Partner - das Positron - dabei (mehr oder weniger) und befindet sich im Vakuum (mehr oder weniger). Neben seiner Masse und Ladung hat es noch eine wichtige Eigenschaft: den Spin. Natürlich sind alle drei Größen gequantelt: Eine Elektronenmasse (mit zwei Vorzeichen) , eine Elementarladung (mit zwei Vorzeichen) und Spin 1/2 (mit zwei Vorzeichen). Zu dumm nur, dass sich das Elektron (und sein Partner) nicht auf ein Vorzeichen einigen können, geschweige denn auf einen Ort, an dem sie zu einer bestimmten Zeit erscheinen wollen...
| Nehmen wir an, das Elektron befindet sich zur Zeit t = 0 innerhalb einer Gaußverteilung (Wellenpaket) um den Ort x = 0. Was macht es dann (im nächsten Moment)? Es bewegt sich - von selbst, bzw. mit Hilfe des Vakuums - nach rechts, dann wieder etwas nach links, nach rechts,... und im Mittel etwas mehr nach rechts, jedenfalls in nebenstehender Abbildung. Das wusste schon Schrödinger (aus heutiger Sicht - zu Unrecht - nur zuständig für das nichtrelativistische Elektron) und nannte es die Zitterbewegung. Insbesondere Dirac und Feynman haben dann das relativistische Elektron näher untersucht (zumindest theoretisch :-)) und die Grundlagen für eine bis heute in ihrer Genauigkeit unübertroffene Theorie gelegt: Die Quantenelektrodynamik (QED). Zu dumm nur, dass sich auch in der QED das Elektron nicht wie ein Kügelchen benimmt, nicht einmal wie ein 'anständiges' nichtrelativistisches Wellenpaket, das einfach nur zerfließt. Vielmehr stellt man fest, dass je nach den Anfangsbedingungen (Energie und Spin positiv oder negativ, bzw. eine Mischung aller vier Möglichkeiten) unterschiedliche Entwicklungen ablaufen, von denen nebenstehend eine gezeigt ist. | 
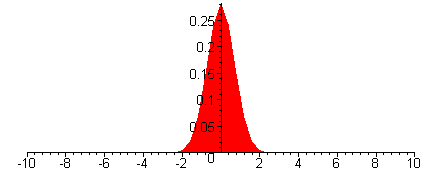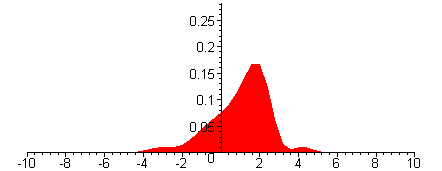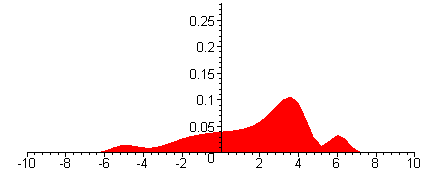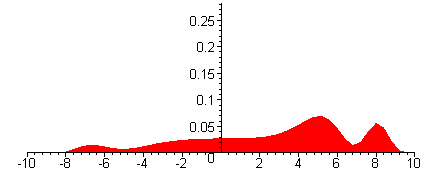
Betragsquadrat der Wellenfunktion |
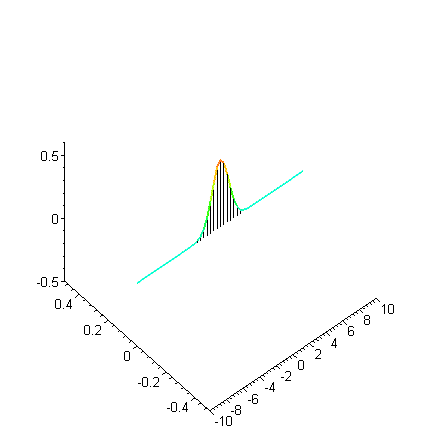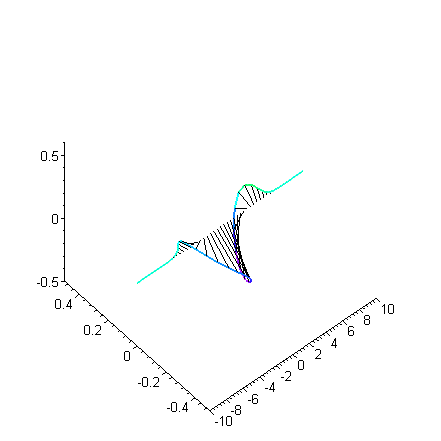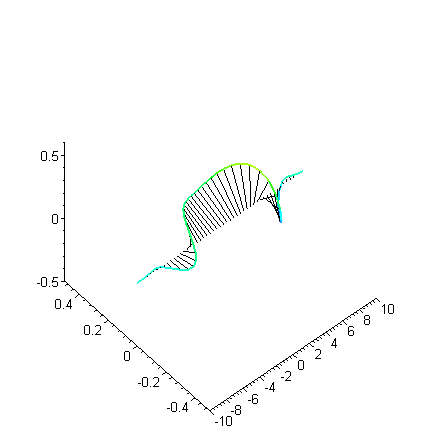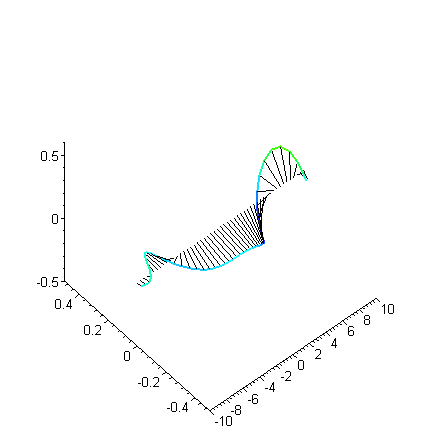
| Das Betragsquadrat der
Wellenfunktion (hier des Spinors) steht für die Wahrscheinlichkeit, das
Elektron zur Zeit t am Ort x (im Film zwischen -10 und 10, in geeigneten
Einheiten) anzutreffen. Es wird aus der komplexen Amplitude (Realteil
vertikal, Imaginärteil horizontal) berechnet. Dazu wurden die
Gleichungen von R. P. Feynman verwendet (Propagator des relativistischen
Elektrons 1949), die eine wichtige Grundlage der Elektron-Positron-Theorie
bilden. Feynmans Beschreibung ist äquivalent zur Theorie Diracs (->
Dirac-Gleichung). Sie bietet aber einen wesentlichen Vorteil, was die
Interpretation der Zitterbewegung angeht: Das Elektron bewegt sich
ständig mit Lichtgeschwindigkeit vorwärts und rückwärts (wenn man die
Zeitskala genügend klein macht). Die makroskopische Bewegung (z.B. 'nach
vorne') ist in diesem Bild ein Ergebnis von 'mehr (zufälligen) Bewegungen
nach vorne als zurück', eben eine Zitterbewegung. Die Amplitude für
einen solchen Pfad ist (I*dt*m)^R (I: Wurzel aus -1, dt: infinitesimales
Zeitintervall, m: Masse des Teilchens, R: Anzahl der Richtungswechsel). In
einem Ort-Zeit-Diagramm bewegt sich das Elektron wie ein Läufer auf einem
Schachbrett (-> Feynmans Checkerboard). Wenn man nun die
Amplituden aller möglichen Pfade (des Läufers von A nach B) geeignet
sortiert, kombiniert und aufsummiert, erhält man die Amplitude für
'Elektron von A nach B'.
Aber VORSICHT: Der Film zeigt die Mathematik der QED in einer sub-sub-atomaren Skala. Das Elektron _ist_ keine komplexe Zahl - oder doch? Man sollte dazu wohl Experimente machen. Am ehesten scheinen dazu Untersuchungen zur Chiralität (~ Spin) des Elektrons geeignet, die auch schon im Gange sind... |
Amplitude |
Siehe auch: Schrödingers Oszillator
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top