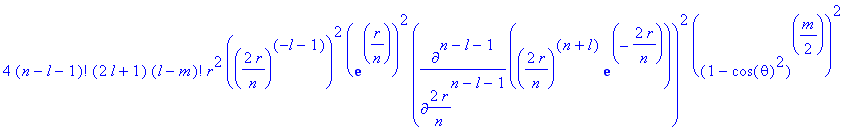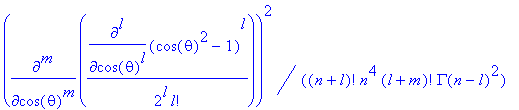Die Wahrscheinlichkeit dafür, ein Elektron im H-Atom im Zustand mit den Quantenzahlen n, l und m bei den Koordinaten r und θ zu finden, ist gegeben durch:
(Die Wahrscheinlichkeitsdichte ist axialsymmetrisch, deswegen wurde der Azimut weggelassen.)
In einem Maple-Worksheet kann man nun Quantenzahlen eingeben und mit einem Zufallszahlengenerator eine Punkteverteilung erzeugen, die dieser Dichte entspricht. Wir versuchen es mit nlm = 300:
![[Maple Plot]](images/h14.gif)
Nach rechts ist der Radius und nach oben ist der Polarwinkel abgetragen. Zur räumlichen Darstellung verteilen wir die Punkte gleichmäßig im Azimut und lassen einen 90°-Sektor rotieren:
![[Maple Plot]](images/h15.gif)
Im realen Maple-Worksheet kann diese Animation in Echtzeitrotation zusätzlich mit der Maus um die horizontale und vertikale Achse gedreht werden, verlangsamt und beschleunigt werden, angehalten werden, anders eingefärbt werden, vergrößert und verkleinert werden, verschieden beleuchtet werden, mit anderen Symbolen dargestellt werden, rückwärts abgespielt werden, in andere Anwendungen kopiert werden,...
Und... mit anderen Parametern neu erzeugt werden!
Zum Inhalt
H-Orbitals aus ' Moderne Physik mit Maple'
|
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top |